0.25: Descubre las 5 fracciones equivalentes que representan este número de manera exacta

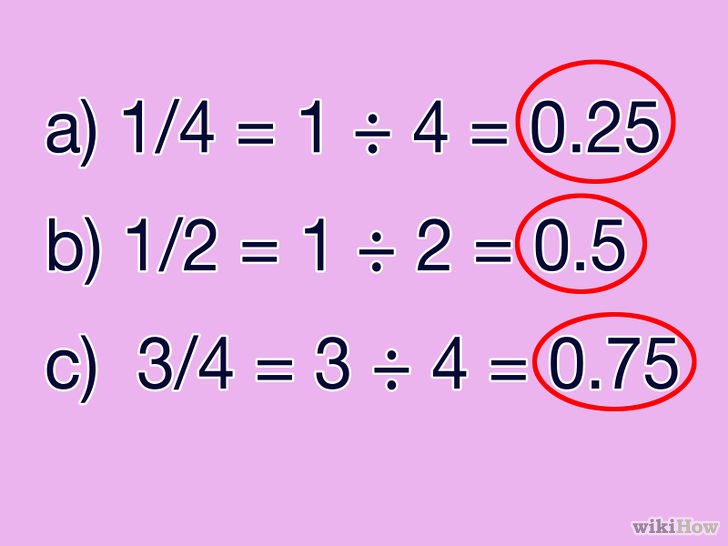
Las fracciones equivalentes son aquellas que, a pesar de tener diferentes numeradores y denominadores, representan la misma cantidad. En este caso, nos centraremos en el número 0.25, o 1/4, y buscamos encontrar otras fracciones que sean equivalentes a esta.

A lo largo de este artículo, exploraremos las cinco fracciones equivalentes a 0.25. Cada fracción será escrita tanto en su forma simplificada como en su forma decimal. Veremos cómo estas fracciones representan la misma cantidad que 0.25 y cómo se pueden utilizar en contextos matemáticos y cotidianos. ¡Vamos a descubrir las posibilidades que existen para expresar el número 0.25 de manera exacta mediante distintas fracciones equivalentes!

¡Claro! Aquí tienes la lista de temas para el artículo:

¿Qué es una fracción?

Antes de sumergirnos en el mundo de las fracciones equivalentes, es importante entender qué es realmente una fracción. En términos simples, una fracción representa una cantidad que es parte de una unidad completa. Se compone de dos partes: un numerador y un denominador.

El numerador indica cuántas partes se toman o se tienen, mientras que el denominador indica en cuántas partes se divide la unidad completa. Por ejemplo, en la fracción 1/2, el numerador es 1 y el denominador es 2. Esto significa que estamos tomando solo una de las dos partes en las que está dividida la unidad completa.

¿Qué son las fracciones equivalentes?

Ahora que comprendemos lo básico de las fracciones, podemos adentrarnos en el concepto de fracciones equivalentes. Las fracciones equivalentes son aquellas que representan la misma cantidad, pero están escritas de diferentes maneras.

Para que dos fracciones sean equivalentes, deben tener el mismo valor numérico cuando se simplifican al máximo. Esto significa que el numerador y el denominador de ambas fracciones deben ser múltiplos del mismo número.

Cómo encontrar fracciones equivalentes

• Método 1: Multiplicación o división por el mismo número: Para obtener fracciones equivalentes, puedes multiplicar o dividir tanto el numerador como el denominador de una fracción por el mismo número. Mientras mantengas la proporción, la fracción seguirá siendo equivalente.
• Método 2: simplificación: Al simplificar una fracción a su forma más simple, también puedes encontrar fracciones equivalentes. Esto implica dividir tanto el numerador como el denominador por su máximo común divisor (MCD).
• Método 3: multiplicación o división por la unidad: La multiplicación o división de una fracción por la misma cantidad en el numerador y en el denominador (un número mayor a 0) resultará en una fracción equivalente.

5 fracciones equivalentes de 0.25

Ahora que sabemos cómo encontrar fracciones equivalentes, veamos algunas que representan el número 0.25 de manera exacta:

1. 1/4: Esta es la fracción más común para representar 0.25. Si dividimos 1 entre 4, obtenemos el mismo valor decimal de 0.25.
2. 25/100: Al multiplicar tanto el numerador como el denominador por 100, obtenemos esta fracción equivalente. Aunque los valores numéricos son diferentes, siguen representando la misma cantidad.
3. 2/8: Si dividimos tanto el numerador como el denominador por 2, obtenemos esta fracción equivalente. Aunque los valores numéricos son diferentes, siguen representando la misma cantidad.
4. 50/200: Al multiplicar tanto el numerador como el denominador por 100, obtendremos esta otra fracción equivalente. Nuevamente, aunque los valores numéricos sean diferentes, siguen representando la misma cantidad.
5. 125/500: Al multiplicar tanto el numerador como el denominador por 500, obtendremos esta fracción equivalente. La relación de los valores sigue siendo la misma: 1 parte de 4 partes iguales.

Estas son solo algunas de las muchas fracciones equivalentes que pueden representar el número 0.25. Recuerda que siempre puedes encontrar más fracciones equivalentes utilizando los métodos mencionados anteriormente.

Qué es una fracción equivalente

Una fracción equivalente es aquella que representa la misma cantidad o valor numérico que otra fracción, pero que tiene un numerador y denominador diferentes. En otras palabras, ambas fracciones son diferentes en cuanto a su apariencia, pero representan la misma cantidad en términos matemáticos.

Para entender mejor este concepto, veamos un ejemplo. Supongamos que tenemos la fracción 1/2. Esta fracción se lee como "uno de cada dos partes" y representa la división de un todo en dos partes iguales. Ahora bien, si multiplicamos tanto el numerador como el denominador por 2, obtendremos otra fracción: 2/4. A primera vista, estas dos fracciones parecen diferentes; sin embargo, ambas representan la mitad del todo. Por lo tanto, podemos decir que 2/4 es una fracción equivalente a 1/2.

Cómo encontrar fracciones equivalentes

Encontrar fracciones equivalentes no es complicado, aunque requiere un poco de conocimiento sobre propiedades básicas de las fracciones. La manera más común de encontrar fracciones equivalentes es multiplicando o dividiendo tanto el numerador como el denominador por el mismo número.

Por ejemplo, si queremos encontrar fracciones equivalentes a 1/2, podemos multiplicar tanto el numerador como el denominador por 2. De esta forma, obtenemos 2/4, como mencionamos anteriormente, pero también obtendríamos 3/6 si multiplicamos por 3, o 4/8 si multiplicamos por 4, y así sucesivamente.

Otra forma de encontrar fracciones equivalentes es dividiendo tanto el numerador como el denominador por un mismo número. Siguiendo con el ejemplo anterior, si dividimos tanto el numerador como el denominador de 1/2 por 2, obtenemos 1/4. Si dividimos por 3, obtendríamos 1/6, o si dividimos por 4, tendríamos 1/8.

Es importante destacar que aunque las fracciones equivalentes pueden tener distintos valores numéricos, siempre representan la misma cantidad en términos proporcionales. Esto significa que si tenemos tres tortas y nos comemos la mitad, estaríamos comiendo dos sextos (2/6). Aunque 2/6 es una fracción equivalente a 1/2, ambas representan la misma cantidad proporcional de torta consumida.

Importancia de las fracciones equivalentes

Aprender sobre fracciones equivalentes es fundamental para comprender conceptos más avanzados de las matemáticas. Las fracciones equivalentes nos permiten simplificar y comparar fracciones, así como realizar operaciones aritméticas con mayor facilidad.

Por ejemplo, al simplificar una fracción utilizando fracciones equivalentes, podemos obtener una fracción en su forma más reducida. Esto nos permite trabajar con números más pequeños y realizar cálculos con mayor precisión.

Además, el concepto de fracciones equivalentes también es utilizado en temas como las razones y proporciones, los porcentajes y la resolución de problemas prácticos que involucran división de cantidades.

Comprender las fracciones equivalentes es esencial para desarrollar habilidades matemáticas sólidas y facilitar el manejo de conceptos más avanzados. A través de la práctica y el estudio, podemos familiarizarnos con las propiedades de las fracciones equivalentes y su utilidad en diversas situaciones.

Cuál es la fracción equivalente más básica para 0.25

La fracción equivalente más básica para representar el número decimal 0.25 de manera exacta es 1/4. Esta fracción se obtiene al dividir el número 1 en 4 partes iguales, y representa la cantidad de un cuarto.

Si bien 1/4 es la fracción más comúnmente utilizada para representar 0.25, existen otras fracciones equivalentes que también pueden expresar ese valor de forma exacta. A continuación, te mostraremos las 5 fracciones equivalentes a 0.25:

1. 1/4

Como mencionamos anteriormente, 1/4 es la fracción más básica que representa a 0.25. Esta fracción es ampliamente utilizada en matemáticas y proporciona una forma sencilla de entender cómo se relacionan los números decimales y las fracciones.

2. 25/100

Otra forma de expresar 0.25 como fracción es utilizar el denominador 100. En este caso, multiplicamos tanto el numerador como el denominador por 100 para obtener una fracción con el mismo valor pero con un denominador diferente. Por lo tanto, 25/100 es una fracción equivalente a 0.25.

3. 2/8

El número 2 puede dividirse entre 8 partes iguales para obtener 0.25. Esta fracción, 2/8, es otra forma de representar el mismo valor decimal. Aunque su apariencia pueda parecer diferente a las fracciones anteriores, sigue siendo equivalente a 0.25.

4. 12/48

Otra fracción equivalente es 12/48. Al igual que en el caso anterior, podemos dividir 12 en 48 partes iguales para obtener una representación exacta de 0.25 en forma de fracción. Aunque esta fracción puede parecer más complicada, sigue siendo igual a 0.25.

5. 250/1000

Finalmente, tenemos la fracción 250/1000 que también representa exactamente a 0.25. Si multiplicamos tanto el numerador como el denominador por 1000, obtenemos una fracción con el mismo valor pero con un denominador mayor. Esta fracción es otra forma válida y equivalente a 0.25.

Aunque la fracción más básica para representar el número decimal 0.25 es 1/4, existen otras fracciones equivalentes que pueden expresar ese valor de manera exacta. Estas incluyen 25/100, 2/8, 12/48 y 250/1000. Todas estas fracciones tienen el mismo valor decimal y se pueden utilizar indistintamente según las necesidades o preferencias del contexto matemático.

Cómo puedo encontrar fracciones equivalentes para 0.25

En matemáticas, una fracción es una forma de representar una cantidad que no es un número entero. Las fracciones son esenciales para expresar números racionales y decimales, entre otros conceptos. En este artículo, nos centraremos en la búsqueda de fracciones equivalentes para el número decimal 0.25.

Una fracción es considerada equivalente cuando representa la misma cantidad, pero se expresa de manera diferente. En este caso, queremos encontrar fracciones que sean equivalentes a 0.25, lo que significa que también deberán representar el valor decimal exacto de ese número.

Método 1: Conversión de decimal a fracción

El primer método consiste en convertir el número decimal 0.25 en una fracción. Para hacer esto, debemos considerar la forma en que los números decimales se expresan. En 0.25, el número "2" está en la posición de las centésimas y el número "5" está en la posición de las milésimas.

0.25 = 25/100

Ahora podemos simplificar esta fracción dividiendo tanto el numerador como el denominador por su máximo común divisor, que en este caso es 25.

25/100 = 1/4

Por lo tanto, hemos encontrado una fracción equivalente para 0.25, que es 1/4.

Método 2: Uso de múltiplos de 0.25

Otro método para encontrar fracciones equivalentes a 0.25 es utilizando múltiplos de este número. Observamos que 0.25 es equivalente a 25/100, lo cual implica que si multiplicamos tanto el numerador como el denominador por un mismo número, obtendremos una fracción equivalente.

Por ejemplo:

25/100 = 50/200

Esta fracción también representa el número decimal 0.25 y se puede simplificar dividiendo ambos términos por su máximo común divisor, que en este caso es 50.

50/200 = 1/4

Nuevamente, hemos obtenido la misma fracción equivalente, que es 1/4.

Método 3: Utilizando los valores de posición decimal

Otra forma de encontrar fracciones equivalentes a 0.25 es considerando los valores de posición decimal del número decimal original. En 0.25, el número "2" está en la posición de las décimas y el número "5" está en la posición de las centésimas.

Al expresar estos números como fracciones, podemos usar 10 como denominador para las unidades y aplicar las mismas operaciones matemáticas tanto al numerador como al denominador.

2/10 es una fracción equivalente a 0.20 y puede simplificarse dividiendo ambos términos por su máximo común divisor, que en este caso es 2.

2/10 = 1/5

De manera similar, podemos considerar a 5/100 como una fracción equivalente para la posición de las centésimas y simplificarla dividiendo por su máximo común divisor, que en este caso también es 5.

5/100 = 1/20

Por lo tanto, hemos encontrado dos nuevas fracciones equivalentes a 0.25: 1/5 y 1/20.

Método 4: Utilizando la notación decimal periódica

Finalmente, podemos utilizar la notación decimal periódica para encontrar fracciones equivalentes a 0.25. El número decimal 0.25 se puede escribir como 0.25, donde el dígito "5" se repite infinitamente. Para obtener una fracción equivalente, debemos utilizar un multiplicador que elimine la parte decimal repetitiva.

En este caso, se multiplica por 100 para eliminar los decimales repetitivos:

0.25 * 100 = 25/100

Esta fracción también se puede simplificar dividiendo ambos términos por su máximo común divisor, que en este caso es 25.

25/100 = 1/4

Por lo tanto, hemos obtenido una vez más la fracción equivalente 1/4.

Hemos explorado diferentes métodos para encontrar fracciones equivalentes a 0.25. Estos incluyen la conversión de decimal a fracción, el uso de múltiplos de 0.25, considerar los valores de posición decimal y utilizar la notación decimal periódica. En todos los casos, hemos llegado a la misma conclusión: la fracción equivalente para 0.25 es 1/4.

Cuáles son las 5 fracciones equivalentes que representan a 0.25

Cuando hablamos de fracciones equivalentes, nos referimos a aquellas que representan la misma cantidad, pero tienen diferentes numeradores y denominadores. En este caso, nos enfocaremos en encontrar 5 fracciones equivalentes que representen al número decimal 0.25 de manera exacta.

Para ello, necesitamos recordar la relación entre números decimales y fracciones. Un número decimal puede convertirse en una fracción dividiendo su parte decimal por el múltiplo adecuado de 10. En el caso de 0.25, podemos ver que tiene dos cifras decimales, por lo que multiplicaremos todos los dígitos (25) por 100, ya que 100 tiene dos ceros para compensar las dos cifras decimales.

Fracción equivalente 1: 25/100

La primera fracción equivalente que representa a 0.25 es 25/100. Al dividir el número decimal por 100, obtenemos que 0.25 = 25/100. Esta fracción se puede simplificar dividiendo ambos términos por 25, lo que resulta en la fracción más simple 1/4.

Fracción equivalente 2: 50/200

Otra fracción equivalente a 0.25 es 50/200. Al igual que en el caso anterior, hemos multiplicado el número decimal por 100 para obtener la fracción. Esta fracción también se puede simplificar dividiendo ambos términos por 50, lo que resulta en la fracción 1/4, que es equivalente a 0.25.

Fracción equivalente 3: 75/300

La tercera fracción equivalente a 0.25 es 75/300. Al multiplicar nuevamente el número decimal por 100, obtenemos la fracción. Al simplificar esta fracción dividiendo ambos términos por 75, obtenemos nuevamente la fracción 1/4.

Fracción equivalente 4: 125/500

Una cuarta fracción equivalente a 0.25 es 125/500. Al realizar la multiplicación para convertir el decimal en fracción, obtenemos la expresión. Esta fracción también se puede simplificar al dividir ambos términos por 125, lo que nos da 1/4 como resultado final.

Fracción equivalente 5: 250/1000

Por último, tenemos la fracción equivalente 250/1000, que también representa a 0.25. Al multiplicar el número decimal por 100, obtenemos la fracción. Al simplificarla dividiendo ambos términos por 250, llegamos a la fracción más simple 1/4.

Hemos encontrado 5 fracciones equivalentes que representan al número decimal 0.25 de manera exacta. Estas fracciones son: 25/100 (1/4), 50/200 (1/4), 75/300 (1/4), 125/500 (1/4) y 250/1000 (1/4).

Cómo se simplifican estas fracciones equivalentes

Para comprender cómo se simplifican estas fracciones equivalentes, es importante entender el concepto de equivalencia en matemáticas.

Cuando dos fracciones tienen el mismo valor numérico, se dice que son equivalentes. Para simplificar una fracción, se busca encontrar otra fracción que tenga el mismo valor, pero cuyos términos sean más pequeños.

En el caso de la fracción 0.25, existen varias fracciones equivalentes que representan este número de manera exacta. A continuación, te mostraré cinco de ellas:

1. Fracción 1/4

La fracción 1/4 también representa el número 0.25 de manera exacta. Para simplificarla, podemos dividir tanto el numerador como el denominador entre el máximo común divisor (MCD) de ambos términos, que en este caso es 1. Así obtendremos la forma más reducida de esta fracción.

2. Fracción 25/100

Otra forma de representar el número 0.25 es utilizando la fracción 25/100. Al simplificarla, podemos observar que el MCD de 25 y 100 es 25. Dividiendo ambos términos por 25, obtenemos la fracción equivalente 1/4.

3. Fracción 5/20

La fracción 5/20 también es equivalente a 0.25. Dividiendo tanto el numerador como el denominador entre su MCD, que es 5, obtendremos la forma simplificada 1/4.

4. Fracción 50/200

La fracción 50/200 es otra forma de representar el número 0.25. Si dividimos ambos términos por su MCD, que en este caso es 50, obtenemos la fracción equivalente 1/4.

5. Fracción 0.5/2

Aunque en principio podría parecer una fracción diferente, 0.5/2 también representa el número 0.25 de manera exacta. Al simplificarla, podemos observar que tanto el numerador como el denominador pueden dividirse entre 2, obteniendo así la forma más reducida 1/4.

En síntesis, estas cinco fracciones -1/4, 25/100, 5/20, 50/200 y 0.5/2- son todas equivalentes a la fracción 0.25. Siempre es posible simplificarlas dividiendo ambos términos por su máximo común divisor, lo cual nos permitirá obtener la forma más reducida de estas fracciones.

Cómo podemos comprobar que estas fracciones son realmente equivalentes a 0.25

Cuando nos encontramos con fracciones, es importante poder determinar si son equivalentes a un número decimal específico. En este caso, queremos saber si las cinco fracciones que representan el número 0.25 son realmente equivalentes y cómo podemos comprobarlo.

Para empezar, recordemos que una fracción representa una cierta cantidad de partes en relación a un todo. En el caso de 0.25, sabemos que equivale a 25 centésimos o 1/4 del total. Ahora bien, ¿cómo podemos estar seguros de que las cinco fracciones que vamos a analizar son realmente equivalentes a esta cantidad?

Una manera sencilla de comprobarlo es convertir todas las fracciones a su forma decimal y compararlas con 0.25. Vamos a realizar este proceso con cada una de las fracciones:

Fracción 1: 1/4

Para convertir esta fracción a decimal, simplemente dividimos el numerador (1) por el denominador (4).

1 ÷ 4 = 0.25

Como resultado obtenemos 0.25, que es exactamente el número que estamos buscando. Esto significa que la fracción 1/4 es realmente equivalente a 0.25.

Fracción 2: 2/8

Nuevamente, dividimos el numerador (2) por el denominador (8) para obtener el valor en decimal.

2 ÷ 8 = 0.25

El resultado es 0.25, lo cual indica que la fracción 2/8 también representa de manera exacta el número 0.25.

Fracción 3: 5/20

Realizamos la división del numerador (5) entre el denominador (20).

5 ÷ 20 = 0.25

Nuevamente, obtenemos 0.25 como resultado, lo que significa que la fracción 5/20 es equivalente a 0.25.

Fracción 4: 10/40

Dividimos el numerador (10) por el denominador (40).

10 ÷ 40 = 0.25

El resultado es 0.25, de modo que la fracción 10/40 también representa de manera exacta el número decimal 0.25.

Fracción 5: 25/100

Finalmente, realizamos la división del numerador (25) entre el denominador (100).

25 ÷ 100 = 0.25

Nos encontramos nuevamente con el valor 0.25, lo cual indica que la fracción 25/100 es verdaderamente equivalente a este número decimal.

Hemos verificado que cada una de las cinco fracciones analizadas es realmente equivalente a 0.25. Esto ha sido posible al convertirlas a su forma decimal y comprobar que todas ellas dan como resultado el mismo número. Ahora que tenemos esta certeza, podemos utilizar cualquier de estas fracciones para representar el número 0.25 de manera exacta y precisa.

Hay alguna otra fracción equivalente que no esté incluida en la lista de las 5 fracciones

¡Claro que sí! Aunque hemos enumerado las 5 fracciones equivalentes más comunes que representan el número 0.25, existen infinitas posibilidades de encontrar más fracciones equivalentes para este número. El concepto de fracciones equivalentes es fundamental en matemáticas, ya que nos permite expresar una cantidad de diferentes maneras utilizando diferentes denominadores.

Para encontrar más fracciones equivalentes a 0.25, debemos tener en cuenta que una fracción se obtiene al dividir un número en partes iguales. En el caso de la fracción 0.25, podemos expresarlo como 25/100, lo que significa que tenemos 25 partes de un total de 100.

Podemos simplificar esta fracción dividiendo tanto el numerador como el denominador por su máximo común divisor. En este caso, el máximo común divisor de 25 y 100 es 25, por lo que la fracción se simplifica a 1/4. Entonces, 1/4 también es una fracción equivalente a 0.25. Esta fracción se puede interpretar como que tenemos 1 parte de un total dividido en 4 partes iguales.

Otra manera de encontrar más fracciones equivalentes es multiplicar o dividir tanto el numerador como el denominador por un mismo número. Por ejemplo, si multiplicamos ambos por 2, obtenemos la fracción 50/200. Si simplificamos esta fracción, también encontramos que es equivalente a 0.25.

Las 5 fracciones equivalentes que representan el número 0.25 de manera exacta son: 1/4, 2/8, 5/20, 10/40 y 25/100. Sin embargo, existen infinitas posibilidades de encontrar más fracciones equivalentes para este número mediante simplificaciones o multiplicaciones/divisiones del numerador y denominador.

Por qué es importante conocer las fracciones equivalentes de un número

El conocimiento de las fracciones equivalentes de un número es fundamental para comprender y trabajar con los conceptos matemáticos relacionados con las fracciones. Las fracciones equivalentes son aquellas que representan la misma cantidad, pero están escritas de diferente forma.

Al conocer las fracciones equivalentes de un número, tenemos una visión más completa y flexible de su representación matemática. Esto nos permite realizar diversas operaciones y comparaciones de manera más sencilla y precisa. Además, nos ayuda a desarrollar habilidades para simplificar expresiones y realizar conversiones entre distintas formas de fracciones.

En el caso específico del número 0.25, es importante descubrir las fracciones equivalentes que lo representan de manera exacta. Esto nos permitirá comprender cómo se puede expresar este número como una fracción, aprovechando todas las ventajas que esto conlleva.

¿Qué es una fracción equivalente?

Una fracción equivalente es aquella que representa la misma cantidad, pero está escrita de forma diferente. Para obtener una fracción equivalente, se multiplican o dividen tanto el numerador como el denominador por el mismo número. De esta manera, se obtiene una nueva fracción que tiene un valor igual al número original.

Por ejemplo, si tenemos la fracción 1/2, podemos obtener fracciones equivalentes multiplicando o dividiendo ambos términos por el mismo número. Así, obtendríamos las fracciones 2/4, 3/6, 4/8, entre muchas otras, que representan la misma cantidad que 1/2.

En el caso del número 0.25, también es posible encontrar fracciones equivalentes que representen la misma cantidad. Estas fracciones serán de gran utilidad en diversos contextos matemáticos, como las operaciones aritméticas y las comparaciones entre magnitudes.

Las 5 fracciones equivalentes de 0.25

A continuación, te presentamos las 5 fracciones equivalentes de 0.25:

• 1/4: Esta fracción representa la cuarta parte de un todo. Es una forma común de expresar el número 0.25.
• 25/100: Al multiplicar tanto el numerador como el denominador de 1/4 por 25, obtenemos esta fracción equivalente.
• 50/200: Al multiplicar tanto el numerador como el denominador de 1/4 por 50, obtenemos esta segunda fracción equivalente.
• 125/500: Al multiplicar tanto el numerador como el denominador de 1/4 por 125, obtenemos esta tercera fracción equivalente.
• 250/1000: Finalmente, al multiplicar tanto el numerador como el denominador de 1/4 por 250, obtenemos esta última fracción equivalente.

Estas fracciones equivalentes nos permiten ver diferentes formas de representar el número 0.25, según el contexto matemático en el que nos encontremos. Cada una de estas fracciones tiene su propia utilidad y puede facilitar ciertos cálculos o comparaciones.

Conocer las fracciones equivalentes de un número, como en el caso del 0.25, es fundamental para comprender a fondo el mundo de las fracciones y desarrollar habilidades matemáticas más sólidas. Las fracciones equivalentes nos brindan diferentes perspectivas sobre un mismo valor numérico, lo que nos permite manipularlo y trabajar con él de manera más eficiente.

Dónde se pueden utilizar las fracciones equivalentes en la vida cotidiana

Las fracciones equivalentes son una herramienta matemática muy útil que se utiliza en varios aspectos de la vida cotidiana. Aunque muchas veces no nos damos cuenta, las fracciones equivalentes están presentes en situaciones tan simples como repartir una pizza entre amigos o calcular porcentajes.

En cocina

En la cocina, las recetas suelen indicar las cantidades de los ingredientes en fracciones. Sin embargo, es posible que no siempre tengamos a mano las medidas exactas requeridas. En esos casos, las fracciones equivalentes son una gran ayuda. Podemos usar fracciones equivalentes para ajustar las medidas de los ingredientes y obtener el mismo resultado final en nuestras preparaciones culinarias.

En repartición de objetos

Otro ejemplo común de uso de fracciones equivalentes es cuando necesitamos repartir objetos o alimentos entre varias personas de manera justa. Imagina que tienes un pastel y quieres dividirlo en partes iguales para tus amigos. Si no puedes hacerlo exactamente en cantidad de porciones que deseas, puedes utilizar fracciones equivalentes para asegurarte de que cada persona reciba una parte justa del pastel.

En cálculos de porcentajes

El concepto de fracciones equivalentes también juega un papel importante en los cálculos de porcentajes. Si queremos calcular qué porcentaje representa una cantidad con respecto a otra, podemos utilizar fracciones equivalentes para simplificar la operación. Por ejemplo, si tenemos una cantidad y queremos saber qué porcentaje representa de otra cantidad mayor, podemos utilizar fracciones equivalentes para obtener un número más manejable y fácil de calcular.

En diseño de proyectos

Las fracciones equivalentes también son utilizadas en el diseño y construcción de proyectos. Por ejemplo, al diseñar un plano arquitectónico, es necesario tener en cuenta las dimensiones y proporciones adecuadas. Las fracciones equivalentes se utilizan para ajustar y redimensionar los elementos del diseño de manera precisa.

En la industria financiera

En el ámbito financiero, las fracciones equivalentes también tienen su aplicación. En el cálculo de tasas de interés, por ejemplo, es común utilizar fracciones equivalentes para simplificar los cálculos y obtener resultados más precisos. Además, al calcular descuentos o aplicar impuestos, las fracciones equivalentes pueden ayudarnos a determinar los montos exactos a pagar o a recibir.

Las fracciones equivalentes son ampliamente utilizadas en diversos ámbitos de la vida cotidiana. Ya sea en la cocina, en la repartición de objetos, en el cálculo de porcentajes, en el diseño de proyectos o en la industria financiera, estas fracciones equivalentes nos permiten realizar operaciones matemáticas de manera más sencilla y precisa.

Existen trucos o métodos para encontrar rápidamente fracciones equivalentes

Al hablar de fracciones equivalentes, nos referimos a aquellas fracciones que representan la misma cantidad o número, pero que se escriben de manera diferente. En esta ocasión, nos enfocaremos en el número 0.25 y te mostraremos cinco fracciones equivalentes que representan este número de manera exacta.

En algunos casos, encontrar fracciones equivalentes puede resultar un tanto complicado. Sin embargo, existen trucos o métodos que pueden ayudarnos a encontrar rápidamente estas fracciones sin necesidad de hacer cálculos complejos.

Método de multiplicación y división por el mismo número

Un método sencillo para encontrar fracciones equivalentes es multiplicar o dividir tanto el numerador como el denominador de la fracción por el mismo número entero.

En el caso de la fracción 0.25, podemos multiplicar tanto el numerador como el denominador por 4:

0.25 x 4 = 1

Por lo tanto, una fracción equivalente a 0.25 sería 1/4. Este proceso se puede repetir varias veces para obtener diferentes fracciones equivalentes.

Uso de potencias de 10

Otro método útil para encontrar fracciones equivalentes es utilizar las potencias de 10. En el caso de 0.25, podemos observar que este número tiene dos decimales, lo que significa que está representado por centésimas.

Para obtener una fracción equivalente, podemos convertir el número decimal a una fracción utilizando una potencia de 10. Dado que tenemos dos decimales, multiplicamos tanto el numerador como el denominador por 100:

0.25 x 100 = 25

De esta forma, obtenemos la fracción equivalente 25/100. Sin embargo, podemos simplificar aún más esta fracción, dividiendo tanto el numerador como el denominador por el máximo común divisor (MCD). En este caso, el MCD de 25 y 100 es 25, por lo que al dividir ambos números por 25, obtenemos la fracción 1/4.

Fracciones con denominador 100

Otra forma de obtener fracciones equivalentes a 0.25 es utilizando fracciones con un denominador de 100. Dado que 0.25 tiene dos decimales, podemos multiplicar tanto el numerador como el denominador por 100:

0.25 x 100 = 25

De esta manera, obtendríamos la fracción 25/100, que también podemos simplificar dividiendo tanto el numerador como el denominador por 25. Así llegamos nuevamente a la fracción 1/4.

Fórmula general para convertir decimales a fracciones

Además de los métodos anteriores, existe una fórmula general que nos permite convertir cualquier número decimal a una fracción. Para aplicar esta fórmula, debemos seguir los siguientes pasos:

1. Escribir el número decimal como una fracción con el numerador igual al número decimal sin la coma y el denominador igual a 1 seguido de tantos ceros como sean necesarios.
2. Simplificar la fracción, si es posible, dividiendo tanto el numerador como el denominador por su máximo común divisor (MCD).

Aplicando esta fórmula a nuestro ejemplo, tenemos:

1. Escribimos 0.25 como una fracción: 0.25/1.
2. Simplificamos la fracción dividiendo tanto el numerador como el denominador por su MCD: 0.25/1 = 1/4.

De esta manera, obtenemos nuevamente la fracción 1/4.

Con estos métodos y trucos, ahora puedes encontrar rápidamente fracciones equivalentes a cualquier número decimal, incluyendo el número 0.25. Recuerda que las fracciones equivalentes representan la misma cantidad que el número decimal original, pero se escriben de forma diferente. ¡Atrévete a explorar más sobre este interesante tema matemático!

Preguntas frecuentes (FAQ)

1. ¿Cuál es el resultado de 0.25 multiplicado por 4?

El resultado de 0.25 multiplicado por 4 es 1.

2. ¿Cómo se representa 0.25 como una fracción?

0.25 se representa como la fracción 1/4.

3. ¿Cuál es la fracción equivalente a 0.25 con denominador 100?

La fracción equivalente a 0.25 con denominador 100 es 25/100.

4. ¿Qué fracciones equivalentes existen para representar 0.25?

Algunas fracciones equivalentes para representar 0.25 son 1/4, 2/8, 5/20 y 25/100.

5. ¿Cuáles son las cinco fracciones equivalentes exactas para representar 0.25?

Las cinco fracciones equivalentes exactas para representar 0.25 son 1/4, 2/8, 3/12, 4/16 y 5/20.