Aprende fácilmente cómo sacar el ángulo de inclinación de una recta en 3 simples pasos

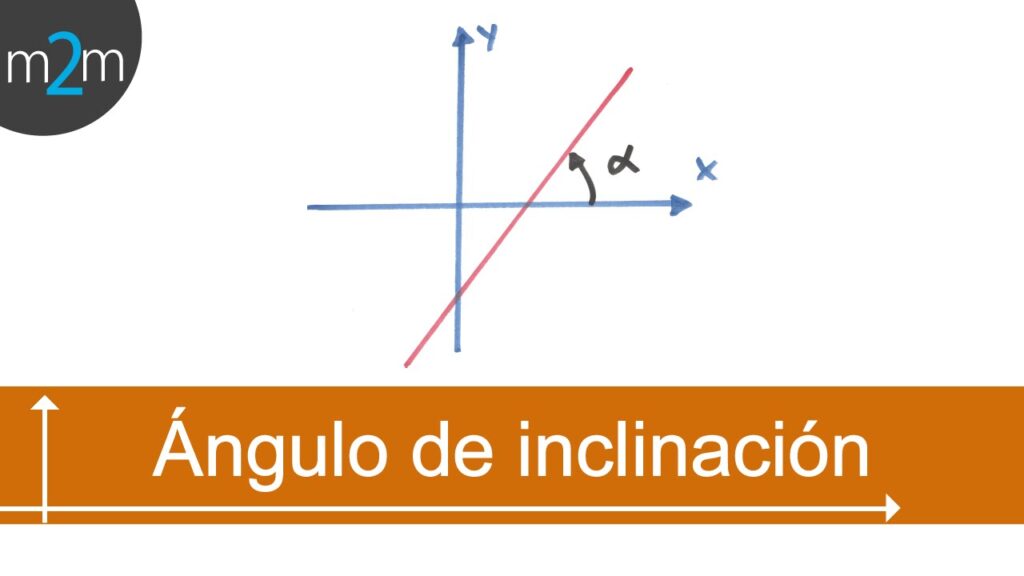
Aprender a sacar el ángulo de inclinación de una recta es una habilidad fundamental en matemáticas y física. El ángulo de inclinación nos permite determinar la pendiente de una recta y comprender su comportamiento. Es especialmente relevante en la trigonometría y en el estudio de funciones lineales.

Te enseñaremos cómo calcular el ángulo de inclinación utilizando tres simples pasos. Exploraremos las fórmulas y conceptos necesarios para realizar el cálculo, así como ejemplos prácticos que te ayudarán a comprender mejor el proceso. Al final, estarás preparado para resolver cualquier problema relacionado con la determinación del ángulo de inclinación de una recta.

Qué es el ángulo de inclinación de una recta y por qué es importante

El ángulo de inclinación de una recta es un concepto fundamental en geometría y trigonometría que nos permite determinar la dirección y pendiente de una línea recta en relación con el eje horizontal. Es la medida angular de la recta respecto a dicho eje y se expresa mediante grados o radianes.

Este ángulo de inclinación es importante en diversos campos como la física, la ingeniería, la arquitectura y la navegación, ya que nos permite comprender y representar visualmente cómo se mueve un objeto o cuerpo en relación con una referencia horizontal.

Cómo calcular el ángulo de inclinación de una recta

A continuación te presentamos un método sencillo y eficaz para calcular el ángulo de inclinación de una recta en tan solo 3 pasos:

1. Paso 1: Selecciona dos puntos en la recta

El primer paso consiste en elegir dos puntos claramente visibles en la recta de la cual queremos determinar su ángulo de inclinación. Estos puntos pueden ser cualquier par de coordenadas (x, y) que pertenezcan a la recta.

2. Paso 2: Calcula la diferencia entre las coordenadas y

Una vez que tienes los dos puntos seleccionados, calcula la diferencia entre sus coordenadas en el eje vertical (y). Resta el valor y del segundo punto al valor y del primer punto. Esto te dará la variación en la coordenada y.

3. Paso 3: Calcula la diferencia entre las coordenadas x

De manera similar al paso anterior, calcula la diferencia entre las coordenadas en el eje horizontal (x) de los dos puntos seleccionados. Resta el valor x del segundo punto al valor x del primer punto. Esto te dará la variación en la coordenada x.

4. Extra: Calcula el ángulo a partir de las diferencias entre las coordenadas

Ahora que tienes las diferencias entre las coordenadas x y y de los dos puntos, es hora de calcular el ángulo de inclinación. Utiliza la fórmula:

Ángulo = arctan(variación en y/variación en x)

Donde arctan es la función arcotangente. Utiliza una calculadora o software matemático para obtener el valor del ángulo en radianes o grados.

Ahora ya conoces cómo sacar el ángulo de inclinación de una recta en 3 simples pasos. ¡Pon en práctica este método y sigue explorando el fascinante mundo de la geometría!

Cuáles son los pasos básicos para sacar el ángulo de inclinación de una recta

Saber cómo sacar el ángulo de inclinación de una recta puede ser útil en muchas áreas, desde las matemáticas hasta la física y la ingeniería. Afortunadamente, este proceso no es tan complicado como parece y se puede realizar en solo 3 sencillos pasos.

Paso 1: Obtener las coordenadas de dos puntos

El primer paso para determinar el ángulo de inclinación de una recta es obtener las coordenadas de dos puntos que pertenezcan a ella. Estos puntos pueden ser cualquier par de puntos sobre la línea recta. Por ejemplo, consideremos los puntos P(x1, y1) y Q(x2, y2).

Paso 2: Calcular la diferencia entre las coordenadas x e y

Una vez que tenemos las coordenadas de los dos puntos, el siguiente paso es calcular la diferencia entre las coordenadas x e y de estos puntos. Para ello, simplemente restamos las coordenadas correspondientes. Es decir:

Δx = x2 - x1
Δy = y2 - y1

Paso 3: Determinar el ángulo de inclinación

Ahora que tenemos las diferencias Δx y Δy, podemos determinar el ángulo de inclinación de la recta utilizando la fórmula:

α = arctan(Δy / Δx)

Donde arctan es la función arcotangente, que nos dará el valor del ángulo en radianes.

Una vez que tengamos el resultado de α, podemos convertirlo a grados multiplicándolo por 180/π.

Es importante tener en cuenta que el resultado del ángulo de inclinación puede ser positivo o negativo dependiendo de la dirección de la línea recta. Un ángulo positivo indica que la recta se inclina hacia arriba, mientras que un ángulo negativo indica que la recta se inclina hacia abajo.

Con estos 3 simples pasos, ahora puedes determinar rápidamente el ángulo de inclinación de una recta. Ya sea que necesites aplicarlo en problemas matemáticos o en tu trabajo como ingeniero o físico, este conocimiento te será de gran utilidad.

Qué información necesito para calcular el ángulo de inclinación de una recta

Para calcular el ángulo de inclinación de una recta, necesitamos contar con ciertos datos clave que nos permitirán realizar los cálculos necesarios. A continuación, te presento la información que debes tener a mano:

• Las coordenadas de dos puntos en la recta. Estos puntos pueden ser cualquiera en la línea recta y deben estar claramente definidos. Por ejemplo, podríamos tener los puntos A(x₁, y₁) y B(x₂, y₂).

Una vez que contemos con esta información, podremos proceder a seguir los siguientes pasos para hallar el ángulo de inclinación de la recta de forma sencilla:

Paso 1: Calcular la diferencia en los valores y

En primer lugar, vamos a calcular la diferencia entre las coordenadas y de los dos puntos dados. Es importante restar el valor y del segundo punto al valor y del primer punto. Utilizaremos la fórmula siguiente:

Δy = y2 - y1

Donde Δy representa el cambio en el valor y.

Paso 2: Calcular la diferencia en los valores x

El siguiente paso consiste en calcular la diferencia entre las coordenadas x de los puntos. Al igual que en el paso anterior, vamos a restar el valor x del segundo punto al valor x del primer punto. La fórmula se expresa de la siguiente manera:

Δx = x2 - x1

Donde Δx representa el cambio en el valor x.

Paso 3: Calcular el ángulo de inclinación

Finalmente, podemos calcular el ángulo de inclinación utilizando la fórmula del arco tangente. La ecuación se muestra a continuación:

α = arctan(Δy / Δx)

Donde α representa el ángulo de inclinación.

Una vez que hayas realizado los cálculos correspondientes, obtendrás el ángulo de inclinación de la recta deseada. Recuerda verificar si el resultado está en radianes o grados dependiendo de tus necesidades.

Cómo se calcula el ángulo de inclinación utilizando la fórmula estándar

Calcular el ángulo de inclinación de una recta puede parecer complicado al principio, pero en realidad es bastante sencillo si sigues estos tres pasos. En este artículo aprenderás cómo utilizar la fórmula estándar para determinar el ángulo de inclinación de una recta.

Paso 1: Identificar los puntos

El primer paso para calcular el ángulo de inclinación es identificar dos puntos en la recta. Estos puntos pueden ser cualquier par de coordenadas (x, y) pertenecientes a la recta. Por ejemplo, podríamos tener los puntos P(2, 4) y Q(5, 9).

Paso 2: Calcular la diferencia entre las coordenadas

Una vez que hemos identificado los puntos, procedemos a calcular la diferencia entre las coordenadas. Para ello, restamos las coordenadas del segundo punto (Q) de las coordenadas del primer punto (P). Tomando el ejemplo anterior, tendríamos:

Δx = x2 - x1 = 5 - 2 = 3
Δy = y2 - y1 = 9 - 4 = 5

Donde Δx representa la diferencia en el eje x y Δy representa la diferencia en el eje y.

Paso 3: Aplicar la fórmula del ángulo de inclinación

Una vez que tenemos las diferencias entre las coordenadas, podemos aplicar la fórmula del ángulo de inclinación. Esta fórmula establece que el ángulo de inclinación se obtiene dividiendo la diferencia en y (Δy) entre la diferencia en x (Δx), es decir:

ángulo de inclinación = Δy / Δx

Tomando el ejemplo anterior, el ángulo de inclinación sería:

ángulo de inclinación = 5 / 3 ≈ 1.67

Por lo tanto, el ángulo de inclinación de la recta que pasa por los puntos P(2, 4) y Q(5, 9) es aproximadamente 1.67.

Recuerda que este cálculo se basa en la fórmula estándar para el ángulo de inclinación y es aplicable a cualquier recta en un plano cartesiano. Ahora que conoces estos tres simples pasos, podrás calcular el ángulo de inclinación de una recta de manera rápida y sencilla.

Hay alguna otra forma de calcular el ángulo de inclinación de una recta

Si bien el cálculo del ángulo de inclinación de una recta se suele hacer utilizando la fórmula tradicional, existe otra forma de calcularlo que puede resultar más sencilla y práctica. Esta alternativa utiliza las coordenadas de dos puntos en la recta para determinar su pendiente y, a partir de ella, obtener el ángulo correspondiente.

Paso 1: Identificar los puntos (x1, y1) y (x2, y2)

En primer lugar, debemos identificar dos puntos en la recta de la cual queremos encontrar su ángulo de inclinación. Llamaremos a estos puntos (x1, y1) y (x2, y2) respectivamente.

Una vez que tengamos claro cuáles son estos puntos, pasaremos al siguiente paso.

Paso 2: Calcular la pendiente de la recta

Para calcular la pendiente de la recta que une los puntos (x1, y1) y (x2, y2), utilizaremos la siguiente fórmula:

m = (y2 - y1) / (x2 - x1)

donde m representa la pendiente.

Una vez aplicada la fórmula, obtendremos un número que nos indicará qué tan inclinada está la recta. Tomaremos nota de este valor, ya que lo necesitaremos en el siguiente paso.

Paso 3: Calcular el ángulo de inclinación

Por último, utilizaremos la pendiente calculada en el paso anterior para obtener el ángulo de inclinación de la recta.

Para ello, aplicaremos la siguiente fórmula:

ángulo = atan(m)

dónde ángulo representa el ángulo de inclinación en radianes.

Una vez realizado este cálculo, podemos convertir el resultado a grados si así lo deseamos, multiplicando el ángulo obtenido por ¹⁸⁰/_π.

Y eso es todo. Con estos tres simples pasos, podemos calcular fácilmente el ángulo de inclinación de una recta utilizando las coordenadas de dos puntos en ella. Esta alternativa puede resultar especialmente útil cuando no se dispone de la ecuación de la recta o cuando se quiere realizar un cálculo más rápido y sencillo.

Cuál es la importancia práctica del ángulo de inclinación en la vida cotidiana

El ángulo de inclinación de una recta es una medida muy importante en diversos campos de la vida cotidiana. Ya sea en la construcción, la ingeniería, la cartografía o incluso en las tareas más simples como colgar cuadros en una pared, comprender cómo sacar el ángulo de inclinación puede resultar sumamente útil.

En la construcción, saber cómo determinar el ángulo de inclinación de una pendiente es fundamental para planificar correctamente la construcción de carreteras, puentes o cualquier otra obra civil. Además, en la ingeniería estructural, es necesario calcular el ángulo de inclinación para diseñar estructuras estables y seguras.

En el campo de la cartografía, el ángulo de inclinación también juega un papel crucial. Permite representar de manera precisa diferentes terrenos en mapas topográficos, lo cual facilita la navegación y ayuda a evitar zonas peligrosas o de difícil acceso.

Incluso en tareas tan simples como colgar cuadros en una pared, el ángulo de inclinación puede marcar la diferencia entre un resultado estético y equilibrado, o uno desprolijo y descuidado. Saber cómo calcular el ángulo correcto asegura que los cuadros queden perfectamente alineados y nivelados, añadiendo armonía a la decoración de un espacio.

Aprender cómo sacar el ángulo de inclinación de una recta puede ser beneficioso tanto a nivel profesional como personal. No importa cuál sea tu área de trabajo o tus intereses, tener conocimientos sobre esta medida te permitirá tomar decisiones informadas y utilizar recursos de manera eficiente.

Por qué es necesario conocer los pasos precisos para calcular el ángulo de inclinación

Calcular el ángulo de inclinación puede parecer un proceso complicado, pero en realidad se puede obtener mediante una serie de pasos sencillos. Conocer estos pasos precisos te ayudará a realizar cálculos rápidos y precisos, evitando errores que podrían llevar a resultados incorrectos o inexactos.

No importa si eres estudiante, profesional o simplemente alguien interesado en aprender sobre matemáticas y geometría, la capacidad de calcular el ángulo de inclinación te permitirá desarrollar habilidades analíticas y de razonamiento lógico.

• Tener claridad sobre los pasos necesarios para calcular el ángulo de inclinación te dará confianza y seguridad al abordar problemas que involucren esta medida.
• Podrás aplicar este conocimiento en situaciones reales, como el diseño de rampas accesibles, la instalación de sistemas de nivelación o incluso en juegos y actividades recreativas que requieran tener una comprensión espacial precisa.
• Comprender cómo sacar el ángulo de inclinación también te permitirá comunicarte con mayor eficacia en diferentes contextos profesionales donde esta medida es relevante.

Conocer los pasos precisos para calcular el ángulo de inclinación no solo te ahorrará tiempo y evitará posibles errores, sino que además te brindará una ventaja tanto en el ámbito académico como en el profesional. No importa cuál sea tu campo de estudio o profesión, este conocimiento te abrirá puertas y te permitirá desarrollar habilidades matemáticas y espaciales fundamentales.

¡Atrévete a aprender cómo sacar el ángulo de inclinación de una recta en 3 simples pasos y descubre las aplicaciones prácticas que este conocimiento puede tener en tu vida diaria!

Qué ocurre si la recta es vertical u horizontal? ¿Cómo afecta esto al cálculo del ángulo de inclinación

Para calcular el ángulo de inclinación de una recta, es importante tener en cuenta si la recta es vertical u horizontal. Esto se debe a que la pendiente de una recta vertical es infinita, mientras que la pendiente de una recta horizontal es cero.

Si nos encontramos con una recta vertical, no podemos calcular su ángulo de inclinación utilizando la fórmula convencional de la pendiente. En cambio, debemos utilizar una forma alternativa para determinar el ángulo. Podemos hacer esto mediante el uso de trigonometría y calculando la tangente del ángulo de inclinación.

Por otro lado, si tenemos una recta horizontal, su ángulo de inclinación es de 0 grados. Esto significa que la recta no tiene ningún tipo de inclinación en relación a la línea horizontal.

Para calcular el ángulo de inclinación de una recta vertical, podemos utilizar la siguiente fórmula:

ángulo de inclinación = arctan(pendiente)

Donde la pendiente de una recta vertical es infinita, por lo que obtendremos un ángulo de 90 grados.

Por otro lado, si queremos calcular el ángulo de inclinación de una recta horizontal, simplemente obtenemos una pendiente de cero y el ángulo de inclinación será igual a cero grados.

Cuando nos encontramos con una recta vertical, su ángulo de inclinación es de 90 grados, mientras que una recta horizontal tiene un ángulo de inclinación de 0 grados. Es importante tener en cuenta estas situaciones especiales al calcular el ángulo de inclinación de una recta para obtener resultados precisos.

Cuál es la relación entre el ángulo de inclinación y la pendiente de una recta

El ángulo de inclinación de una recta es una medida que indica la pendiente o la inclinación de la misma. Es una magnitud muy importante en la geometría y la trigonometría, ya que nos permite comprender y analizar las propiedades y características de las rectas en un plano cartesiano.

Para entender la relación entre el ángulo de inclinación y la pendiente de una recta, debemos recordar que la pendiente se define como el cociente entre la variación vertical y la variación horizontal de dos puntos en la recta. Es decir:

pendiente = (y2 - y1) / (x2 - x1)

El ángulo de inclinación se puede obtener a partir de la pendiente utilizando funciones trigonométricas, específicamente la tangente. La fórmula para calcular el ángulo de inclinación es:

ángulo = arctan(pendiente)

Donde arctan es la función inversa de la tangente.

Pasos para sacar el ángulo de inclinación de una recta

A continuación, te presento tres sencillos pasos para calcular el ángulo de inclinación de una recta:

• Paso 1: Deducir la pendiente de la recta.
• Paso 2: Aplicar la función arctan a la pendiente calculada en el paso anterior.
• Paso 3: Obtener el valor del ángulo de inclinación en radianes o convertirlo a grados si es necesario.

Recuerda que la pendiente puede ser positiva, negativa o cero, lo cual afectará el rango de valores del ángulo de inclinación. Si la pendiente es positiva, el ángulo de inclinación será agudo, si es negativa, el ángulo será obtuso y si es cero, la recta estará horizontal y el ángulo de inclinación será de 0 o 180 grados.

Ahora que conoces la relación entre el ángulo de inclinación y la pendiente de una recta, así como los pasos para calcularlo, podrás aplicar esta fórmula en diferentes problemas de geometría y trigonometría. Recuerda practicar y resolver ejercicios para afianzar tus conocimientos y habilidades en este tema.

Existen aplicaciones o herramientas en línea que pueden ayudarme a calcular el ángulo de inclinación de una recta

Calcular el ángulo de inclinación de una recta puede ser un proceso complicado si no tienes los conocimientos y las herramientas adecuadas. Afortunadamente, en la era digital en la que vivimos, existen diversas aplicaciones y herramientas en línea que pueden facilitarte este cálculo en solo unos pocos pasos.

Estas aplicaciones y herramientas son especialmente útiles para aquellos que trabajan en campos como la arquitectura, la ingeniería civil o la geometría, donde el cálculo de ángulos de inclinación es fundamental para la resolución de problemas y el diseño de estructuras.

¿En qué consiste el cálculo del ángulo de inclinación?

Antes de sumergirnos en las aplicaciones y herramientas disponibles, es importante comprender qué es el ángulo de inclinación de una recta y cómo se calcula.

El ángulo de inclinación de una recta es la medida en grados del ángulo que forma con el eje x positivo. Básicamente, nos indica qué tan empinada o inclinada está la recta en relación a dicho eje.

Para calcular el ángulo de inclinación de una recta, generalmente se utiliza la fórmula:

m = (y2 - y1) / (x2 - x1)

Donde (x1, y1) y (x2, y2) son dos puntos conocidos en la recta y m representa la pendiente de la recta.

Una vez que se ha calculado la pendiente, se puede encontrar el ángulo de inclinación utilizando la función inversa de la tangente (tan^-1). Esta función devuelve el ángulo cuya tangente es igual a la pendiente de la recta.

Aplicaciones y herramientas en línea para calcular el ángulo de inclinación

Ahora que entendemos cómo se calcula el ángulo de inclinación de una recta, veamos algunas de las aplicaciones y herramientas disponibles en línea que pueden ayudarnos con esta tarea:

• Calculadoras en línea: Existen numerosas calculadoras en línea que te permiten ingresar los puntos conocidos en la recta y automáticamente calculan la pendiente y el ángulo de inclinación. Algunas de estas calculadoras incluso ofrecen opciones adicionales, como graficar la recta o proporcionar explicaciones detalladas del proceso de cálculo.
• Aplicaciones móviles: Si prefieres utilizar tu dispositivo móvil, también hay diferentes aplicaciones disponibles tanto para iOS como para Android que hacen el cálculo del ángulo de inclinación rápido y sencillo. Estas aplicaciones suelen ser intuitivas, con interfaces amigables y algunas incluso tienen opciones para guardar tus cálculos o compartirlos.
• Herramientas de software: Para aquellos que trabajan de manera más profesional o necesitan realizar cálculos frecuentes, existen herramientas de software específicas que ofrecen funciones avanzadas para el cálculo de ángulos de inclinación. Estas herramientas suelen ser más complejas y están diseñadas para profesionales del campo, pero también pueden ser muy útiles para estudiantes o entusiastas de la geometría.

Independientemente de la opción que elijas, es importante recordar que estas aplicaciones y herramientas son solo una ayuda para facilitar el proceso de cálculo. Es fundamental comprender los conceptos detrás del cálculo del ángulo de inclinación y cómo se obtiene cada resultado.

Si estás buscando calcular el ángulo de inclinación de una recta de manera fácil y rápida, no dudes en utilizar las aplicaciones y herramientas en línea disponibles. Estas te permitirán ahorrar tiempo y esfuerzo, para que puedas concentrarte en resolver problemas más complejos y emocionantes en tu campo de trabajo.

Cuáles son las aplicaciones del conocimiento sobre el ángulo de inclinación de una recta en diferentes campos, como la arquitectura, la ingeniería o la geometría

El ángulo de inclinación de una recta es un concepto fundamental en diferentes campos, como la arquitectura, la ingeniería o la geometría. Es utilizado para medir la inclinación o pendiente de una línea recta con respecto a un eje de referencia.

En el campo de la arquitectura, el conocimiento sobre el ángulo de inclinación de una recta es crucial al diseñar estructuras y edificios. Permite determinar la inclinación de techos, escaleras, rampas o cualquier otra superficie inclinada. Conociendo el ángulo de inclinación, los arquitectos pueden asegurarse de que las estructuras estén correctamente alineadas y cumplan con los estándares de seguridad necesarios.

En la ingeniería, el ángulo de inclinación de una recta es utilizado en diversos campos, como la construcción de carreteras, puentes y ferrocarriles. Al tener en cuenta este ángulo, los ingenieros pueden calcular la resistencia y estabilidad de las estructuras, así como asegurarse de que cumplan con las normativas y regulaciones establecidas.

En geometría, el ángulo de inclinación de una recta proporciona información importante sobre las relaciones entre líneas rectas. Se utiliza para determinar si dos rectas son paralelas, perpendiculares o simplemente oblicuas entre sí. Además, el ángulo de inclinación también se utiliza para resolver problemas de trigonometría, donde se necesita conocer la inclinación de una línea en relación a un punto de referencia.

La importancia de calcular el ángulo de inclinación de una recta con precisión

Calcular el ángulo de inclinación de una recta con precisión es fundamental en todos estos campos. Un pequeño error en el cálculo puede tener grandes consecuencias en la construcción de estructuras o en la resolución de problemas geométricos. Además, el conocimiento preciso del ángulo de inclinación también permite optimizar diseños y mejorar la eficiencia en diferentes áreas.

Los pasos para sacar el ángulo de inclinación de una recta con facilidad

1. Identifica dos puntos en la recta: primero, selecciona dos puntos claramente definidos en la recta de la cual deseas encontrar el ángulo de inclinación. Estos puntos deben ser distintos y pueden estar ubicados en cualquier posición de la recta.
2. Calcula la diferencia entre las coordenadas de los dos puntos: utilizando las coordenadas de los dos puntos identificados en el paso anterior, determina la diferencia entre las coordenadas x e y de ambos puntos. Esta diferencia representa el cambio vertical (Δy) y horizontal (Δx) en la recta.
3. Aplica la fórmula del ángulo de inclinación: finalmente, utiliza las diferencias calculadas en el paso anterior y aplica la fórmula del ángulo de inclinación. Esta fórmula consiste en tomar la tangente inversa de la razón entre el cambio vertical y el cambio horizontal (Δy / Δx).

Una vez que hayas seguido estos simples pasos, habrás encontrado el ángulo de inclinación de la recta deseada. Recuerda siempre verificar tus cálculos y asegurarte de utilizar las unidades de medida apropiadas.

El conocimiento sobre el ángulo de inclinación de una recta tiene aplicaciones amplias y diversas en diferentes campos. Ya sea en arquitectura, ingeniería o geometría, comprender y calcular con precisión este concepto es fundamental para el diseño, construcción y resolución de problemas técnicos.

Preguntas frecuentes (FAQ)

1. ¿Cómo se calcula el ángulo de inclinación de una recta?

El ángulo de inclinación de una recta se calcula dividiendo la diferencia en las coordenadas $Δy$ y $Δx$ entre dos puntos de la recta.

2. ¿Puedo calcular el ángulo de inclinación si solo tengo un punto de la recta?

No, necesitas al menos dos puntos en la recta para poder calcular su ángulo de inclinación.

3. ¿Cuál es el ángulo de inclinación de una recta horizontal?

La pendiente de una línea horizontal es cero, por lo tanto, el ángulo de inclinación es cero grados.

4. ¿Cuál es el ángulo de inclinación de una recta vertical?

La pendiente de una línea vertical es infinita, por lo tanto, el ángulo de inclinación no está definido.

5. ¿Qué significa un ángulo de inclinación negativo?

Un ángulo de inclinación negativo indica que la recta está inclinada hacia abajo o de derecha a izquierda en un plano cartesiano.