Calcula el recorrido de una función: Descubre cómo encontrar todos los valores posibles

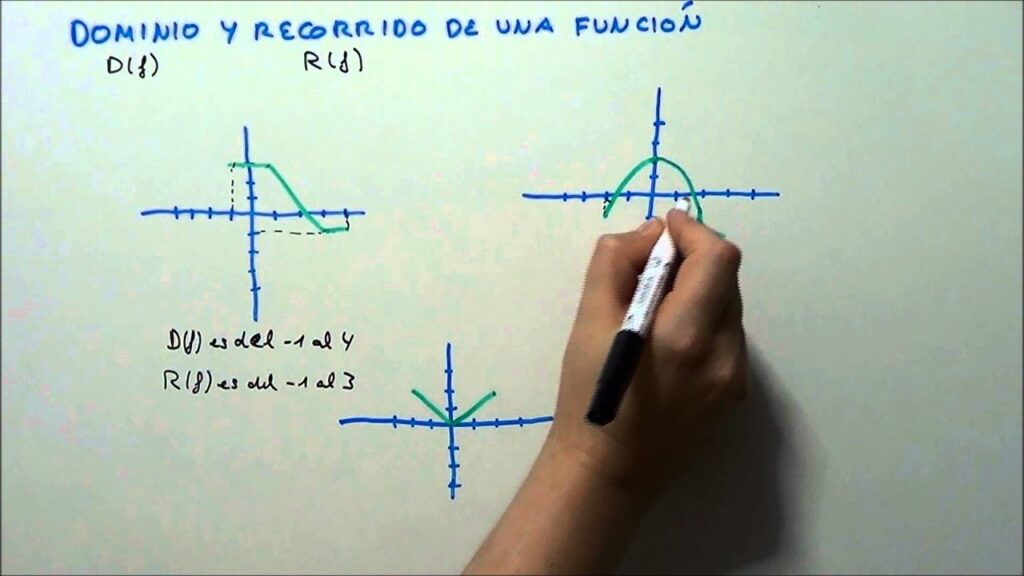
Al estudiar funciones matemáticas, uno de los conceptos más importantes es el recorrido de la función. El recorrido se refiere a todos los valores posibles que la función puede tomar en su conjunto de salida. Comprender y calcular el recorrido de una función es fundamental para comprender su comportamiento y propiedades.

Exploraremos cómo calcular el recorrido de una función paso a paso. Veremos diferentes métodos y técnicas que puedes utilizar, dependiendo del tipo de función que estés trabajando. Además, también discutiremos algunas consideraciones importantes y ejemplos prácticos para ayudarte a tener una mejor comprensión de este concepto clave en el estudio de las funciones matemáticas.

Qué es el recorrido de una función y por qué es importante calcularlo

El recorrido de una función es un concepto fundamental en matemáticas que nos permite determinar todos los valores posibles que la función puede tomar. Es decir, es el conjunto de todos los resultados que obtenemos al evaluar la función para distintos valores de entrada.

Calcular el recorrido de una función es importante porque nos ayuda a comprender mejor su comportamiento y sus posibles salidas. Además, nos permite identificar si existen valores específicos que la función no puede alcanzar.

Para calcular el recorrido de una función, debemos tener en cuenta tanto el dominio de la función (es decir, los valores de entrada válidos) como la regla o fórmula que define la relación entre los valores de entrada y salida.

Encontrar el recorrido de una función paso a paso

A continuación, te mostraremos los pasos que debes seguir para calcular el recorrido de una función:

1. Identifica el dominio de la función: El dominio son todos los posibles valores de entrada que la función acepta. Pueden ser números reales, enteros, fracciones, o cualquier otro tipo de valor dependiendo del contexto.
2. Aplica la regla de la función a cada elemento del dominio: Utiliza la regla de la función para evaluarla en cada uno de los valores del dominio. Este paso puede requerir cálculos algebraicos, sustituciones o simplificaciones, dependiendo de la naturaleza de la función.
3. Registra los valores obtenidos: A medida que vayas evaluando la función en los distintos valores del dominio, registra los resultados obtenidos. Estos valores formarán parte del recorrido de la función.
4. Verifica si hay valores que no pertenecen al recorrido: Después de haber evaluado la función en todos los valores del dominio, verifica si existen valores adicionales que no estén en el conjunto de resultados obtenidos. Estos valores indicarían que la función no puede alcanzar ciertos valores de salida.

Es importante destacar que el cálculo del recorrido de una función puede variar dependiendo del tipo y la complejidad de la función. Algunas funciones más simples pueden tener un recorrido fácil de determinar, mientras que otras pueden requerir técnicas más avanzadas como el análisis matemático o gráfico.

Calcular el recorrido de una función nos permite conocer todos los valores posibles que la función puede tomar. Es un proceso fundamental para comprender su comportamiento y sus limitaciones, además de ser un elemento clave en diversos campos de estudio como la matemática, la física y la informática.

Cuál es la diferencia entre dominio y recorrido de una función

Antes de adentrarnos en cómo calcular el recorrido de una función, es importante comprender la diferencia entre el dominio y el recorrido de una función. Estos dos conceptos son fundamentales en el estudio de las funciones matemáticas.

El dominio de una función se refiere al conjunto de todos los valores de entrada que cumplen ciertas restricciones para que la función esté definida. Es decir, son los valores de x para los cuales la función tiene sentido matemático y produce un resultado válido. El dominio puede ser cualquier conjunto de números o incluso intervalos continuos.

Por otro lado, el recorrido de una función se refiere al conjunto de todos los valores de salida posibles de una función dada. En otras palabras, son los valores de y que la función puede tomar después de evaluar todos los posibles valores de x en su dominio.

Es importante destacar que no todos los valores de y pueden pertenecer al recorrido de una función. Existen casos en los que la función puede estar restringida a ciertos valores o rangos debido a limitaciones matemáticas o físicas.

Cómo encontrar el recorrido de una función

• Paso 1: Determinar el dominio de la función
• Paso 2: Evaluar la función para diferentes valores de x en su dominio
• Paso 3: Registrar todos los valores de y obtenidos en el paso 2
• Paso 4: Eliminar cualquier valor repetido en el conjunto de valores de y
• Paso 5: Ordenar los valores de y en orden ascendente

El primer paso para encontrar el recorrido de una función es determinar su dominio. Para hacer esto, debemos prestar atención a cualquier restricción en la función, como divisiones por cero o raíces cuadradas de números negativos que resulten en valores imaginarios.

Una vez que se ha establecido el dominio, podemos evaluar la función para diferentes valores de x dentro de ese dominio. Es importante tener en cuenta que al evaluar la función, los valores de y pueden ser positivos, negativos o incluso cero.

A medida que evaluamos la función para diferentes valores de x, registramos todos los valores de y correspondientes en un conjunto. Esto se hace para asegurarnos de no omitir ningún valor posible del recorrido.

Después de obtener todos los valores de y posibles, eliminamos cualquier duplicado que pueda existir en el conjunto. Esto nos dará un conjunto único de valores de y que son válidos para la función.

Finalmente, ordenamos los valores de y en orden ascendente para tener una representación más clara del recorrido. Esto nos permitirá visualizar fácilmente el rango de valores que puede tomar la función después de evaluar todos los valores de x en su dominio.

El cálculo del recorrido de una función implica determinar su dominio, evaluar la función para diferentes valores de x, registrar los valores de y correspondientes, eliminar duplicados y ordenar los valores en orden ascendente. Al seguir estos pasos, podemos encontrar todos los valores posibles que la función puede tomar, lo cual es de gran importancia en diversas aplicaciones matemáticas y científicas.

Cómo encontrar todos los valores posibles en el recorrido de una función

El recorrido de una función es el conjunto de todos los valores posibles que la función puede tomar. Al encontrar estos valores, podemos tener una idea clara de cómo se comporta la función y qué resultados puede generar en diferentes entradas. En este artículo, exploraremos algunos métodos para calcular el recorrido de una función y cómo aplicarlos en diferentes escenarios.

1. Identificar el dominio de la función

Antes de buscar los valores posibles en el recorrido de una función, es fundamental comprender el dominio de la misma. El dominio de una función es el conjunto de todas las posibles entradas que pueden ser evaluadas por la función. Por ejemplo, si tenemos una función f(x) = √(x), el dominio sería el conjunto de todos los números reales no negativos (∀ x ≥ 0).

Una vez que hemos identificado el dominio de la función, podemos comenzar a explorar los valores posibles en su recorrido.

2. Graficar la función

Una representación gráfica de la función nos puede proporcionar información valiosa sobre su comportamiento y los valores que puede tomar. Al graficar la función, podemos visualizar la forma de la curva y determinar cualquier patrón o tendencia que pueda tener.

Por ejemplo, si tenemos una función cuadrática f(x) = x^2, al graficarla notaremos que la curva tiene una concavidad hacia arriba y que conforme x se acerca al infinito positivo o negativo, los valores de y también tienden al infinito positivo. Además, podemos observar que la función toma todos los valores reales no negativos en su recorrido.

3. Utilizar técnicas de análisis algebraico

Además de la representación gráfica, existen técnicas de análisis algebraico que nos pueden ayudar a encontrar los valores posibles en el recorrido de una función. Estas técnicas varían dependiendo del tipo de función que estemos trabajando.

Para funciones polinómicas, podemos utilizar propiedades como el grado del polinomio y las raíces para determinar si hay algún límite en los valores posibles en su recorrido.

En caso de una función racional, debemos considerar las restricciones de dominio, ya que pueden existir valores para los cuales la función no está definida. Además, debemos buscar los puntos de discontinuidad y evaluar los límites en estos puntos para determinar los valores posibles en el recorrido.

En funciones exponenciales y logarítmicas, es importante analizar las propiedades de crecimiento y decrecimiento de la función, así como las asíntotas verticales y horizontales, para identificar los valores posibles en su recorrido.

4. Evaluar casos particulares

Algunas funciones pueden tener casos particulares que requieren una evaluación individual. Por ejemplo, si tenemos una función trigonométrica f(x) = sen(x), sabemos que el rango es , por lo que el recorrido se limita a esos valores. Sin embargo, si tenemos una función trigonométrica con desplazamiento, como f(x) = sen(x+π/2), debemos considerar el desplazamiento al momento de encontrar los valores posibles en su recorrido.

En estos casos particulares, es importante utilizar propiedades específicas de las funciones y aplicarlas para determinar los valores posibles en el recorrido.

5. Utilizar software matemático

Afortunadamente, existen numerosos programas de software matemático que nos pueden ayudar a calcular y visualizar el recorrido de una función de manera rápida y precisa. Estos programas nos permiten ingresar la función y obtener un gráfico de la misma, así como los valores posibles en su recorrido.

Algunos ejemplos populares de software matemático incluyen Wolfram Alpha, Geogebra y Matlab. Estas herramientas pueden ser especialmente útiles cuando se trata de funciones más complejas o cuando necesitamos realizar cálculos más precisos.

Calcular el recorrido de una función requiere comprender su dominio, graficarla, aplicar técnicas de análisis algebraico, evaluar casos particulares y, en algunos casos, utilizar software matemático. Al seguir estos pasos, podemos descubrir todos los valores posibles en el recorrido de una función y obtener una comprensión más completa de su comportamiento.

Cuáles son las técnicas básicas para calcular el recorrido de una función

El recorrido de una función es un concepto fundamental en matemáticas que nos permite determinar todos los posibles valores que puede tomar una función. Es decir, el conjunto de todos los valores de salida que la función puede producir cuando se le asignan distintos valores de entrada.

Calcular el recorrido de una función puede ser útil en diversos contextos, como la resolución de ecuaciones, la optimización de problemas o el análisis de comportamiento de fenómenos naturales. Para realizar este cálculo, existen diversas técnicas básicas que podemos utilizar.

1. Expresión algebraica

La forma más sencilla de calcular el recorrido de una función es utilizar su expresión algebraica. Si la función está dada por una fórmula, podemos analizar esta fórmula para determinar qué valores puede tomar la variable independiente y, a partir de eso, obtener los posibles valores de la variable dependiente.

Por ejemplo, si tenemos la función f(x) = x^2, sabemos que la variable independiente x puede tomar cualquier valor real, por lo tanto, el recorrido de la función será todos los posibles valores de x al cuadrado (es decir, todos los números reales no negativos).

2. Análisis de dominio

Otra técnica útil para calcular el recorrido de una función es analizar su dominio. El dominio de una función son todos los valores de entrada posibles, es decir, aquellos valores para los cuales la función está definida.

Al analizar el dominio de una función, podemos determinar qué valores están excluidos y, por lo tanto, no formarán parte del recorrido de la función.

3. Gráfica de la función

Una técnica visualmente intuitiva para calcular el recorrido de una función es observar su gráfica. La gráfica nos muestra cómo se comporta la función en todo su dominio y nos permite identificar los valores que toma a lo largo del eje vertical.

Si la gráfica muestra que la función se extiende hasta infinito en algún sentido, entonces sabemos que el recorrido también incluirá esos valores extremos.

4. Uso de software matemático

Por último, una opción más avanzada para calcular el recorrido de una función es utilizar software matemático especializado. Estos programas pueden ayudarnos a analizar y representar gráficamente las funciones, así como proporcionar resultados precisos y detallados sobre su recorrido.

Existen diversos software matemáticos disponibles en el mercado, como Matlab, Mathematica o Geogebra, que pueden facilitar enormemente el proceso de cálculo del recorrido.

Calcular el recorrido de una función nos permite conocer todos los posibles valores que puede tomar. Para ello, podemos utilizar técnicas básicas como el análisis de la expresión algebraica, el dominio de la función, la gráfica o incluso software matemático especializado. Estas herramientas nos ayudarán a comprender mejor el comportamiento de las funciones y realizar un análisis más completo y preciso.

Qué significan los términos "mínimo" y "máximo" en relación al recorrido de una función

ar los puntos críticos de la función, que son aquellos puntos donde su derivada es igual a cero o no está definida. También se deben considerar los límites cuando la variable tiende hacia el infinito.

Una vez identificados los puntos críticos y los límites, se evalúa la función en cada uno de ellos para determinar cuál es el valor mínimo. El punto donde la función alcanza este valor mínimo se denomina punto de mínimo absoluto.

¿Y cómo encontrar el valor máximo de una función?

Para encontrar el valor máximo de una función, se siguen los mismos pasos que para encontrar el valor mínimo. Se buscan los puntos críticos y los límites, se evalúa la función en cada uno de ellos y se determina cuál es el valor máximo.

Es importante destacar que el valor mínimo y máximo de una función pueden ser únicos o existir varios. En el caso de que existan varios valores mínimos o máximos, se denominan mínimo/máximo local. Por otro lado, si solo hay un valor mínimo o máximo, se denominan mínimo/máximo absoluto.

En conclusión, el valor mínimo y máximo de una función son los puntos más bajos y altos que puede alcanzar respectivamente. Para encontrarlos, se deben buscar los puntos críticos y evaluar la función en ellos, junto con los límites.

Cuáles son las propiedades importantes a tener en cuenta al calcular el recorrido de una función

Para calcular el recorrido de una función, es importante tener en cuenta algunas propiedades fundamentales que nos permitirán encontrar todos los valores posibles. Estas propiedades nos ayudarán a determinar el rango de la función, es decir, el conjunto de todos los valores que la función puede tomar.

Una de las primeras propiedades importantes a considerar es la continuidad de la función. Una función continua es aquella que no tiene saltos o discontinuidades en su gráfica. Si una función es continua en un intervalo determinado, entonces el recorrido estará dado por todos los valores que la función toma en ese intervalo.

Otra propiedad relevante es la existencia de puntos extremos. Estos puntos corresponden a los máximos y mínimos de la función. Si una función tiene un máximo o mínimo absoluto, significa que no tomará valores superiores o inferiores a esos puntos. Por lo tanto, estos puntos formarán parte del recorrido de la función.

Además, es necesario considerar los puntos de inflexión. Estos puntos son aquellos en los que la concavidad de la curva cambia. Si una función tiene puntos de inflexión, los valores correspondientes a estos puntos deben ser incluidos en el recorrido.

También es importante analizar los límites de la función. Los límites nos indican cómo se comporta la función cuando el valor de la variable independiente tiende hacia cierto valor. Si existen límites infinitos o hacia algún número específico, esos valores deben ser considerados en el recorrido.

Finalmente, debemos tener en cuenta cualquier restricción impuesta a la función. Algunas funciones tienen restricciones en el dominio o en el conjunto de valores posibles. Estas restricciones pueden limitar el recorrido de la función, eliminando ciertos valores.

Para calcular el recorrido de una función, debemos considerar la continuidad de la función, los puntos extremos, los puntos de inflexión, los límites y cualquier restricción existente. Teniendo en cuenta todas estas propiedades, podremos encontrar todos los valores posibles que la función puede tomar.

Cuándo debemos considerar restricciones adicionales al calcular el recorrido de una función

Al calcular el recorrido de una función, es importante considerar si existen restricciones adicionales que debamos tomar en cuenta. Estas restricciones pueden surgir por diferentes razones y afectarán los valores posibles que la función puede tomar.

Una restricción común a considerar es el dominio de la función. El dominio es el conjunto de valores para los cuales la función está definida. Si una función tiene un dominio restringido, esto puede limitar los valores posibles que pueda tomar y, por lo tanto, afectar su recorrido. Por ejemplo, si la función está definida solo para valores positivos, entonces todos los valores negativos están excluidos de su recorrido.

Otra restricción puede ser la existencia de asíntotas verticales u horizontales. Una asíntota vertical es una línea vertical a la cual la función se aproxima infinitamente a medida que x tiende hacia un valor específico. Si una función tiene una asíntota vertical en cierto punto, entonces los valores de la función no podrán cruzar esa línea y esto debe ser considerado al determinar su recorrido. Lo mismo ocurre con las asíntotas horizontales, pero en lugar de ser líneas verticales, son líneas horizontales.

Además, algunas funciones pueden tener restricciones específicas impuestas por el contexto del problema o la aplicación en la que se utilizan. Por ejemplo, puede haber restricciones de tiempo, espacio u otras condiciones físicas o matemáticas que limiten los valores posibles de la función. Estas restricciones adicionales deben tomarse en cuenta cuando se busca calcular el recorrido.

Al calcular el recorrido de una función, es crucial considerar cualquier restricción adicional que pueda existir. Estas restricciones pueden incluir el dominio de la función, asíntotas verticales u horizontales, o restricciones específicas relacionadas con el contexto del problema. Al tener en cuenta estas restricciones, podemos determinar con precisión los valores posibles que la función puede tomar y obtener una comprensión más completa de su recorrido.

Cuál es el papel de los límites en el cálculo del recorrido de una función

En el cálculo del recorrido de una función, los límites juegan un papel crucial. Los límites nos permiten determinar los valores a los que se aproxima una función cuando su variable independiente se acerca a ciertos valores específicos. Esto es especialmente útil cuando queremos identificar los valores que la función puede tomar en determinadas regiones

Para calcular el recorrido de una función, necesitamos considerar tres elementos clave: el dominio de la función, los intervalos críticos y los límites.

Dominio de la función

El dominio de una función se refiere al conjunto de todos los posibles valores de entrada, es decir, a qué valores puede tomar la variable independiente. Al determinar el dominio de una función, debemos tener en cuenta las restricciones inherentes a la función, como por ejemplo, las divisiones por cero o las raíces cuadradas de números negativos.

Es importante recordar que el dominio está relacionado directamente con el recorrido de la función. Si hay valores que no están permitidos en el dominio, entonces tampoco podrán existir en el recorrido de la función.

Intervalos críticos

Los intervalos críticos son los puntos en los que la función experimenta cambios en su comportamiento. Estos puntos generalmente se encuentran donde la función cambia de concavidad o presenta discontinuidades.

Para identificar los intervalos críticos, podemos estudiar la primera y segunda derivada de la función. La primera derivada nos dará información sobre los puntos críticos y la dirección en la que la función está creciendo o decreciendo. La segunda derivada nos dará información sobre la concavidad de la función.

Al conocer los intervalos críticos, podremos determinar qué valores son posibles en esos puntos y así ampliar nuestra comprensión del recorrido de la función.

Límites

Finalmente, para calcular el recorrido de una función, debemos evaluar los límites en puntos donde la función pueda tener comportamientos especiales, como asíntotas verticales u horizontales.

Los límites nos permiten identificar los valores que la función se está acercando cuando su variable independiente tiende a un determinado valor. Esto es especialmente útil para descubrir los valores extremos que la función puede tomar en los extremos de su dominio o en puntos donde existan asintotas.

Calcular los límites implica utilizar técnicas de cálculo como límites algebraicos, límites trigonométricos o límites por racionalización, entre otros. Estas técnicas nos permitirán determinar con precisión los valores a los que se aproxima la función, lo cual nos ayudará a encontrar todos los valores posibles en su recorrido.

Para calcular el recorrido de una función, debemos considerar el dominio de la función, los intervalos críticos y los límites en puntos especiales. Mediante el estudio de estos elementos, seremos capaces de determinar con precisión todos los valores posibles que la función puede tomar. El cálculo del recorrido de una función es fundamental para comprender su comportamiento y aplicarlo en diferentes contextos matemáticos y científicos.

Cómo podemos utilizar gráficos o tablas para ayudarnos a calcular el recorrido de una función

Calcular el recorrido de una función es esencial para comprender el comportamiento de la misma y determinar todos los valores posibles para su imagen. Podemos utilizar gráficos o tablas para ayudarnos en este proceso y obtener resultados precisos.

Utilizando gráficos

Los gráficos son una herramienta visual poderosa que nos permite representar gráficamente una función y analizar su comportamiento. Para calcular el recorrido de la función utilizando un gráfico, debemos seguir estos pasos:

• Dibujar el gráfico de la función en un sistema de coordenadas, asegurándonos de incluir todos los puntos relevantes.
• Observar el tramo del eje vertical (eje y) que corresponde al rango de la función.
• Analizar si existen valores límites en este tramo del eje y.
• Determinar si la función es creciente o decreciente en diferentes intervalos y cómo esto afecta al rango.

Al seguir estos pasos, podemos obtener una idea clara de qué valores están incluidos en el recorrido de la función.

Utilizando tablas

Otra forma de calcular el recorrido de una función es utilizando tablas. Esta metodología puede ser especialmente útil cuando no contamos con un gráfico disponible. Para hacerlo:

1. Selecciona una serie de valores para la variable independiente (x) de la función.
2. Calcula los correspondientes valores de la variable dependiente (y) aplicando la función a cada uno de los valores seleccionados.
3. Registra los pares ordenados (x, y) en una tabla.
4. Analiza los valores obtenidos en la tabla y determina cuáles son los posibles valores de la función.

Es importante tener en cuenta que al utilizar tablas, es posible que nos perdamos algunos valores intermedios o puntos críticos. Sin embargo, esta metodología sigue siendo útil para obtener una idea general del recorrido de la función.

En resumen

Ya sea utilizando gráficos o tablas, calcular el recorrido de una función nos brinda información valiosa sobre los valores de imagen posibles para esa función. Ambas metodologías tienen sus pros y sus contras, por lo que es recomendable utilizarlas en conjunto para obtener resultados más precisos.

Recuerda que el recorrido de una función puede ser infinito, finito o incluso puede no existir en ciertos casos. Por tanto, es fundamental comprender bien los conceptos de rango y dominio de una función antes de iniciar el cálculo de su recorrido.

Qué pasa si tenemos una función con múltiples variables? ¿Cómo afecta esto al cálculo del recorrido

El cálculo del recorrido de una función puede volverse más complejo cuando tenemos múltiples variables en juego. En este caso, debemos considerar todas las combinaciones posibles de los valores de estas variables para determinar todos los valores posibles que la función puede tomar.

Combinaciones de variables

Cuando tenemos más de una variable en una función, podemos combinar los diferentes valores de estas variables para obtener nuevas entradas. Por ejemplo, si tenemos dos variables, "x" e "y", podemos combinar los valores de "x" e "y" para obtener pares ordenados como (1, 2), (3, 4), etc.

El número total de combinaciones posibles depende de la cantidad de valores distintos que cada variable puede tomar. Si tenemos n valores posibles para la variable "x" y m valores posibles para la variable "y", entonces tendremos un total de n * m combinaciones posibles.

Encontrar los valores posibles de la función

Una vez que tenemos todas las combinaciones posibles de las variables, podemos encontrar los valores correspondientes de la función. Para hacer esto, simplemente reemplazamos los valores de las variables en la función y realizamos las operaciones necesarias.

Por ejemplo, si tenemos una función f(x, y) = 2x + y, y las siguientes combinaciones posibles de las variables: (1, 2), (3, 4), (5, 6), podemos calcular los valores de la función de la siguiente manera:

f(1, 2) = 2(1) + 2 = 4
f(3, 4) = 2(3) + 4 = 10
f(5, 6) = 2(5) + 6 = 16

De esta manera, encontramos que los valores posibles de la función f(x, y) son 4, 10 y 16.

Representación gráfica

Además de calcular los valores posibles de una función con múltiples variables, también podemos representar estos valores en un gráfico. En el caso de dos variables, podemos usar un sistema de coordenadas cartesianas para representar los pares ordenados obtenidos a partir de las combinaciones de variables.

En nuestro ejemplo anterior, obtuvimos las combinaciones (1, 2), (3, 4) y (5, 6). Podemos dibujar estos puntos en un plano cartesiano y trazar una línea o curva suave a través de ellos para visualizar cómo varían los valores de la función.

Esto nos permite tener una comprensión visual del recorrido de la función con respecto a las diferentes combinaciones de las variables. También nos ayuda a identificar cualquier patrón o tendencia en los valores de la función.

El cálculo del recorrido de una función con múltiples variables puede ser más desafiante debido a la necesidad de considerar todas las combinaciones posibles de los valores de estas variables. Sin embargo, siguiendo los pasos mencionados anteriormente, podemos determinar todos los valores posibles que la función puede tomar.

Además del cálculo, también podemos representar los valores en un gráfico para tener una comprensión visual del recorrido de la función. Esta representación gráfica nos permite analizar patrones y tendencias en los valores de la función.

Al calcular el recorrido de una función con múltiples variables, debemos considerar todas las combinaciones posibles de los valores de estas variables y luego reemplazar estos valores en la función para obtener los valores correspondientes. Además, podemos representar estos valores en un gráfico para una mejor comprensión visual.

Preguntas frecuentes (FAQ)

¿Qué es el recorrido de una función?

El recorrido de una función es el conjunto de todos los valores posibles que puede tomar la función.

¿Cómo puedo encontrar el recorrido de una función?

Para encontrar el recorrido de una función, debes reemplazar la variable independiente por distintos valores y calcular los correspondientes valores de la función. Luego, determina cuáles son los valores únicos obtenidos.

¿Cuál es la diferencia entre el dominio y el recorrido de una función?

El dominio de una función se refiere a los valores que puede tomar la variable independiente, mientras que el recorrido se refiere a los valores que puede tomar la variable dependiente.

¿Es posible que el recorrido de una función sea infinito?

Sí, es posible que el recorrido de una función sea infinito si la función no tiene límites superiores o inferiores en su rango de valores posibles.

¿Cómo puedo representar gráficamente el recorrido de una función?

Puedes representar gráficamente el recorrido de una función trazando una línea o curva que pase por todos los puntos posibles que la función puede tomar. Estos puntos corresponden al recorrido de la función.