Descubre cómo calcular el ángulo de un triángulo rectángulo de forma sencilla y precisa

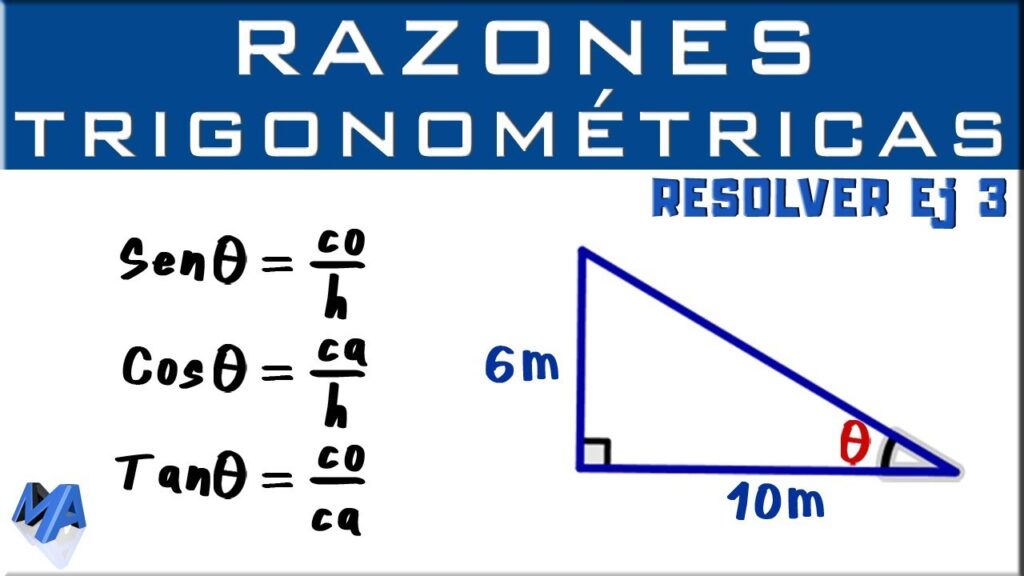
Los triángulos rectángulos son un tipo de figura geométrica muy común y tienen propiedades especiales que los distinguen de otros triángulos. Uno de los elementos más importantes de un triángulo rectángulo es el ángulo recto, que mide 90 grados. Pero además del ángulo recto, también existen otros ángulos en un triángulo rectángulo que pueden ser de interés, ya sea para resolver problemas matemáticos o calcular medidas en la vida diaria.

En este artículo exploraremos cómo calcular el ángulo de un triángulo rectángulo cuando se conocen las medidas de sus lados. Veremos una fórmula específica que nos permitirá obtener dicha medida de forma rápida y precisa. Además, también aprenderemos sobre algunas aplicaciones prácticas de calcular ángulos en triángulos rectángulos y cómo utilizar esta información de manera útil en la resolución de problemas. Si estás interesado en la geometría y quieres saber cómo trabajar con ángulos en triángulos rectángulos, ¡sigue leyendo!

Qué es un triángulo rectángulo y por qué es importante calcular su ángulo

Un triángulo rectángulo es un tipo de triángulo que posee un ángulo recto, es decir, un ángulo de 90 grados. Es uno de los casos más comunes en la geometría y tiene propiedades especiales que lo hacen fundamental para la resolución de problemas matemáticos y aplicaciones prácticas.

Calcular el ángulo de un triángulo rectángulo es importante porque nos permite determinar diferentes aspectos del triángulo, como la longitud de sus lados o la medida de otros ángulos. Además, es útil en situaciones cotidianas donde necesitamos realizar mediciones precisas o resolver problemas de diseño o construcción.

Fórmula para calcular el ángulo de un triángulo rectángulo

Para calcular el ángulo de un triángulo rectángulo, podemos utilizar diferentes métodos y fórmulas. Uno de los más utilizados es el teorema de Pitágoras, el cual establece una relación entre los lados del triángulo:

c^2 = a^2 + b^2

• a y b representan las longitudes de los catetos del triángulo.
• c representa la longitud de la hipotenusa, el lado opuesto al ángulo recto.

Una vez que conocemos las longitudes de dos de los lados del triángulo rectángulo, podemos aplicar esta fórmula para encontrar el valor de la tercera longitud. Luego, podemos utilizar funciones trigonométricas como el seno, coseno o tangente para determinar el valor del ángulo.

Ejemplo de cálculo del ángulo de un triángulo rectángulo

Supongamos que tenemos un triángulo rectángulo con los catetos a = 3 y b = 4. Podemos utilizar el teorema de Pitágoras para encontrar la longitud de la hipotenusa:

c^2 = 3^2 + 4^2
c^2 = 9 + 16
c^2 = 25

Aplicando raíz cuadrada a ambos lados de la ecuación, obtenemos:

c = √25
c = 5

Una vez que conocemos la longitud de la hipotenusa, podemos utilizar la función trigonométrica inversa del seno, coseno o tangente para calcular el ángulo correspondiente. Por ejemplo, si queremos encontrar el ángulo α, podemos usar la función seno:

sen(α) = a / c
sin(α) = 3 / 5

Aplicando la función inversa al seno, obtendremos el ángulo:

α = arcsen(3 / 5)
α ≈ 36.87°

De esta manera, hemos calculado el ángulo α del triángulo rectángulo con catetos 3 y 4, el cual resulta ser aproximadamente 36.87 grados.

Recuerda que la precisión en el cálculo del ángulo dependerá de la precisión en la medición de las longitudes de los lados del triángulo. Por lo tanto, siempre es recomendable utilizar instrumentos de medición confiables y asegurarse de realizar las operaciones matemáticas correctamente.

Cuál es la ecuación básica para calcular el ángulo de un triángulo rectángulo

Para calcular el ángulo de un triángulo rectángulo, es necesario utilizar la relación trigonométrica conocida como tangente. Esta relación nos permite relacionar los lados del triángulo y los ángulos que lo conforman.

La ecuación básica para calcular el ángulo de un triángulo rectángulo es la siguiente:

tan(ángulo) = longitud del cateto opuesto / longitud del cateto adyacente

Esta ecuación nos indica que la tangente de un ángulo en un triángulo rectángulo es igual a la longitud del cateto opuesto dividida por la longitud del cateto adyacente.

Por qué es importante calcular el ángulo de un triángulo rectángulo

Calcular el ángulo de un triángulo rectángulo es fundamental para resolver problemas y aplicaciones en diversos campos, como la física, la geometría y la navegación. Conocer los ángulos de un triángulo nos permite determinar diversas propiedades y relaciones entre sus elementos.

Por ejemplo, si estamos resolviendo un problema de navegación marítima, conocer el ángulo de elevación de un faro desde nuestro punto de referencia nos permitirá determinar nuestra posición exacta en el océano. Si estamos estudiando la geometría de un edificio, conocer los ángulos internos de sus triángulos rectángulos nos permitirá determinar la inclinación de las paredes y la altura de los techos.

Calcular el ángulo de un triángulo rectángulo es una habilidad fundamental en diversas disciplinas y nos brinda información valiosa sobre la forma y las propiedades de los objetos que estamos estudiando.

Cómo utilizar la ecuación básica para calcular el ángulo de un triángulo rectángulo

Para utilizar la ecuación básica tan(ángulo) = cateto opuesto / cateto adyacente, debemos tener los valores de la longitud del cateto opuesto y la longitud del cateto adyacente. Estos valores pueden ser medidos directamente o pueden ser proporcionados en el enunciado del problema.

Una vez que tengamos los valores de los catetos, podemos utilizar una calculadora científica o una tabla de funciones trigonométricas para determinar el valor de la tangente del ángulo deseado.

Una vez que tengamos el valor de la tangente del ángulo, podemos utilizar las funciones inversas de la tangente, conocidas como arcotangentes, para determinar el valor del ángulo en sí.

Es importante recordar que las funciones trigonométricas son periódicas, por lo que puede haber múltiples soluciones para un mismo problema. Por lo tanto, es necesario tener en cuenta las restricciones del problema y elegir la solución que se ajuste mejor a las condiciones dadas.

Ejemplo de cálculo del ángulo de un triángulo rectángulo

Supongamos que tenemos un triángulo rectángulo con un cateto opuesto de longitud 4 cm y un cateto adyacente de longitud 3 cm. Queremos calcular el ángulo formado por estos catetos.

Utilizando la ecuación tan(ángulo) = cateto opuesto / cateto adyacente, reemplazamos los valores conocidos:

tan(ángulo) = 4 cm / 3 cm

Ahora, utilizando una calculadora científica o una tabla de funciones trigonométricas, determinamos el valor de la tangente del ángulo buscado:

tan(ángulo) ≈ 1.33333

Finalmente, utilizamos la función inversa de la tangente para encontrar el valor del ángulo en sí:

ángulo ≈ atan(1.33333)

El valor aproximado del ángulo es de aproximadamente 53.13 grados.

Calcular el ángulo de un triángulo rectángulo es fundamental para resolver problemas y aplicaciones en diversas disciplinas. Utilizando la ecuación básica de la tangente y las funciones trigonométricas, podemos determinar con precisión el ángulo deseado.

Cómo se puede utilizar el teorema de Pitágoras para calcular el ángulo de un triángulo rectángulo

El teorema de Pitágoras es una herramienta matemática fundamental para resolver problemas relacionados con triángulos rectángulos. A través de este teorema, se establece una relación entre las longitudes de los catetos y la hipotenusa de un triángulo rectángulo.

Para utilizar el teorema de Pitágoras y calcular el ángulo de un triángulo rectángulo, es necesario tener información acerca de las longitudes de dos de sus lados. Generalmente, estos lados son conocidos como catetos y se representan mediante las letras "a" y "b", mientras que la hipotenusa se representa con la letra "c".

Paso 1: Identificar los catetos y la hipotenusa

Lo primero que debemos hacer es identificar los catetos y la hipotenusa del triángulo rectángulo. Los catetos son los dos lados más cortos que forman el ángulo recto, mientras que la hipotenusa es el lado más largo y opuesto al ángulo recto.

En nuestro triángulo rectángulo, llamaremos a uno de los catetos "a" y al otro cateto "b". La hipotenusa la representaremos como "c".

Paso 2: Aplicar el teorema de Pitágoras

Una vez que tenemos claros los nombres de los catetos y la hipotenusa, podemos aplicar el teorema de Pitágoras. Este afirma que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

a^2 + b^2 = c^2

Para calcular el ángulo de un triángulo rectángulo, podemos utilizar esta fórmula para determinar la longitud del lado desconocido. Luego, aplicaremos las funciones trigonométricas inversas (seno, coseno o tangente) para encontrar el valor del ángulo correspondiente.

Paso 3: Encontrar el ángulo utilizando las funciones trigonométricas inversas

• Si conocemos los catetos "a" y "b", podemos calcular la hipotenusa "c" utilizando la fórmula anterior. Luego, utilizaremos la función seno, coseno o tangente inversa dependiendo del ángulo que queramos encontrar.
• Por ejemplo, si queremos calcular el ángulo opuesto al cateto "a", utilizaremos la función seno inversa:

ángulo = arcsin(a/c)

• Para calcular el ángulo opuesto al cateto "b", utilizaremos la función coseno inversa:

ángulo = arccos(b/c)

• Y si queremos calcular el ángulo agudo entre los dos catetos, utilizaremos la función tangente inversa:

ángulo = arctan(a/b)

Es importante tener en cuenta que las funciones trigonométricas inversas devuelven el ángulo en radianes. Para obtener el resultado en grados, simplemente debemos aplicar la conversión correspondiente utilizando la siguiente fórmula:

ángulo_en_grados = ángulo_en_radianes * (180 / pi)

Ahora que conoces cómo utilizar el teorema de Pitágoras y las funciones trigonométricas inversas, puedes calcular con precisión el ángulo de un triángulo rectángulo. Recuerda que es fundamental tener claridad sobre los catetos y la hipotenusa del triángulo para aplicar correctamente las fórmulas mencionadas. ¡Diviértete descubriendo nuevos ángulos!

Cuál es la relación entre los lados del triángulo rectángulo y su ángulo opuesto

Cuando nos enfrentamos a un triángulo rectángulo, una de las primeras cosas que queremos conocer es el valor del ángulo opuesto a uno de los lados. Este ángulo es fundamental para poder resolver múltiples problemas de geometría y trigonometría. Afortunadamente, calcular el ángulo de un triángulo rectángulo de forma sencilla y precisa no es tan complicado como podría parecer.

Para entender cómo calcular este ángulo, primero debemos comprender la relación existente entre los lados del triángulo rectángulo y su ángulo opuesto. Esta relación se basa en una de las principales razones por las cuales estos triángulos son tan especiales: el teorema de Pitágoras.

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Matemáticamente, podemos expresar esta relación de la siguiente manera:

a^2 + b^2 = c^2

Donde 'a' y 'b' son las longitudes de los catetos del triángulo y 'c' es la longitud de la hipotenusa. Esta ecuación es clave para nuestro objetivo de calcular el ángulo.

Cómo encontrar el ángulo usando funciones trigonométricas

Una vez que conocemos las longitudes de los lados del triángulo rectángulo, podemos utilizar las funciones trigonométricas básicas para encontrar el ángulo deseado. En particular, nos centraremos en la función tangente (tan).

La tangente de un ángulo se define como la relación entre el cateto opuesto al ángulo y el cateto adyacente. En nuestro caso, el cateto opuesto es la longitud de uno de los lados y el cateto adyacente es la longitud del otro lado.

Matemáticamente, la función tangente se expresa de la siguiente manera:

tan(θ) = o/a

Donde θ representa el ángulo que queremos calcular, 'o' es la longitud del cateto opuesto, y 'a' es la longitud del cateto adyacente. En este caso, si conocemos las longitudes de los catetos, podemos despejar el valor de θ reemplazando los valores correspondientes en la ecuación.

Ejemplo práctico: cálculo del ángulo de un triángulo rectángulo

Imaginemos que tenemos un triángulo rectángulo con un cateto opuesto de longitud 4 y un cateto adyacente de longitud 3. Nuestra tarea es calcular el ángulo que se encuentra opuesto al lado de longitud 4.

Aplicando la función tangente, reemplazamos los valores conocidos en la ecuación:

tan(θ) = 4/3

Para despejar el ángulo, simplemente utilizamos la función inversa de la tangente (atan), también conocida como arcotangente:

θ = atan(4/3)

Utilizando una calculadora o una tabla de valores trigonométricos, podemos obtener que el valor aproximado de θ es de 53.13 grados.

Entonces, en nuestro triángulo rectángulo, el ángulo opuesto al lado de longitud 4 es de aproximadamente 53.13 grados.

Calcular el ángulo de un triángulo rectángulo puede parecer un desafío, pero conociendo las relaciones entre los lados y aplicando las funciones trigonométricas adecuadas, podemos resolverlo de manera sencilla y precisa. Recuerda siempre verificar tus resultados y, si es necesario, utilizar herramientas como calculadoras o tablas de valores trigonométricos para obtener resultados más exactos. ¡Ahora ya sabes cómo calcular el ángulo de un triángulo rectángulo!

Existen otras fórmulas o métodos alternativos para calcular el ángulo de un triángulo rectángulo

Además de utilizar la fórmula clásica para calcular el ángulo de un triángulo rectángulo, existen otras formas que pueden resultar igualmente sencillas y precisas. Estos métodos alternativos pueden ser especialmente útiles en situaciones donde no se cuenta con todas las medidas necesarias o cuando se desea una forma más rápida de obtener el ángulo deseado.

Método del cociente trigonométrico tangente

Uno de los métodos más comunes para calcular el ángulo de un triángulo rectángulo es utilizando la función trigonométrica de la tangente. La tangente de un ángulo se define como la razón entre el cateto opuesto y el cateto adyacente a dicho ángulo.

Para aplicar este método, necesitamos conocer la medida de los catetos del triángulo. Supongamos que tenemos un triángulo rectángulo con un cateto opuesto de longitud "a" y un cateto adyacente de longitud "b". Para calcular el ángulo definido por estos catetos, podemos utilizar la siguiente fórmula:

tangente(ángulo) = a / b

Una vez que conocemos el valor del cociente a / b, podemos encontrar el ángulo correspondiente utilizando la función inversa de la tangente (arco tangente o atan).

Por ejemplo, si tomamos un triángulo rectángulo con un cateto opuesto de longitud 4 y un cateto adyacente de longitud 3, podemos calcular el ángulo utilizando:

tangente(ángulo) = 4 / 3

Para obtener el valor del ángulo, debemos aplicar la función inversa de la tangente:

ángulo = atan(4 / 3)

Este método es especialmente útil cuando conocemos la longitud de los catetos y queremos calcular el ángulo sin necesidad de utilizar las funciones trigonométricas seno o coseno.

Método basado en la fórmula de Pitágoras

Otro método alternativo para calcular el ángulo de un triángulo rectángulo es utilizando la famosa fórmula de Pitágoras. Esta fórmula establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los catetos.

Si conocemos la longitud de dos lados del triángulo rectángulo (ya sea la hipotenusa y un cateto, o ambos catetos), podemos utilizar la fórmula de Pitágoras para determinar el valor del tercer lado. Luego, podemos utilizar las funciones trigonométricas seno, coseno o tangente para calcular el ángulo deseado.

Por ejemplo, si tenemos un triángulo rectángulo con una hipotenusa de longitud 5 y un cateto de longitud 3, podemos calcular el valor del segundo cateto utilizando la fórmula de Pitágoras:

cateto² = hipotenusa² - cateto²
cateto² = 5² - 3²
cateto² = 25 - 9
cateto = √16
cateto = 4

Una vez que tenemos el valor de los catetos, podemos utilizar las funciones trigonométricas mencionadas anteriormente para calcular el ángulo.

Estos son solo dos ejemplos de métodos alternativos para calcular el ángulo de un triángulo rectángulo. En general, es importante recordar que las diferentes fórmulas y métodos pueden ser útiles en diferentes situaciones, dependiendo de la información de que se disponga y del tipo de cálculo requerido. Según el contexto y las necesidades específicas, podemos optar por uno u otro método para obtener resultados precisos y confiables.

Cuáles son algunos ejemplos prácticos de aplicación de cálculo de ángulos en triángulos rectángulos

El cálculo de los ángulos en los triángulos rectángulos es una habilidad matemática fundamental que se utiliza en una amplia variedad de aplicaciones prácticas. Estas aplicaciones abarcan desde la ingeniería y la arquitectura hasta la navegación marítima y la astronomía.

Ingeniería

En el campo de la ingeniería, el cálculo preciso de los ángulos en los triángulos rectángulos es esencial para el diseño y construcción de estructuras como puentes y edificios. Por ejemplo, al determinar los ángulos internos de un triángulo rectángulo formado por las barras de soporte de un puente, los ingenieros pueden asegurar la estabilidad y resistencia adecuada de la estructura.

Arquitectura

Los arquitectos también utilizan el cálculo de los ángulos en los triángulos rectángulos para diseñar y construir edificios. Al calcular los ángulos internos de las paredes, techos y pisos, los arquitectos pueden garantizar una distribución equilibrada de las cargas estructurales y una apariencia estéticamente agradable del edificio.

Navegación marítima

En la navegación marítima y la aviación, el cálculo de los ángulos en los triángulos rectángulos es vital para determinar la ubicación y orientación de un barco o avión en relación con puntos de referencia conocidos. Los navegantes utilizan instrumentos como el sextante para medir los ángulos entre el horizonte y astros como el sol o las estrellas, lo que les permite calcular su posición exacta en el océano.

Astronomía

Los astrónomos también hacen uso del cálculo de los ángulos en los triángulos rectángulos para estudiar y comprender el universo. Al calcular los ángulos formados por la luz emitida por diferentes objetos celestes, los astrónomos pueden determinar sus distancias relativas y características físicas, lo que contribuye a nuestro conocimiento sobre el espacio y el cosmos.

El cálculo de los ángulos en los triángulos rectángulos es una herramienta matemática fundamental con aplicaciones prácticas en diversos campos. Ya sea en ingeniería, arquitectura, navegación marítima o astronomía, comprender cómo calcular con precisión estos ángulos nos permite diseñar, construir y navegar de manera segura y precisa en nuestro entorno.

Cuál es la importancia de conocer el ángulo de un triángulo rectángulo en diferentes disciplinas, como la arquitectura o la ingeniería

Calcular el ángulo de un triángulo rectángulo puede ser de gran importancia en diversas disciplinas, como la arquitectura y la ingeniería. En estos campos, es fundamental contar con medidas precisas y exactas para diseñar estructuras seguras y eficientes.

En la arquitectura, por ejemplo, conocer el ángulo de un triángulo rectángulo puede ser crucial al momento de diseñar techos inclinados o escaleras. Al calcular correctamente los ángulos, se garantiza una construcción estable y funcional.

Por otro lado, en la ingeniería civil, la precisión en los cálculos angulares de los triángulos rectángulos es esencial para determinar las dimensiones adecuadas de puentes, edificios y otras estructuras. Un error en el cálculo de los ángulos podría resultar en estructuras inseguras o mal diseñadas.

Técnicas para calcular el ángulo de un triángulo rectángulo

Existen diferentes métodos para calcular el ángulo de un triángulo rectángulo, dependiendo de la información disponible. A continuación, se presentan algunas técnicas comunes:

1. Teorema del seno: Este teorema establece que en un triángulo rectángulo, el cociente entre la longitud de un cateto y la hipotenusa es igual al seno del ángulo opuesto al cateto. Utilizando este teorema, es posible despejar el valor del ángulo deseado.
2. Teorema del coseno: Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Utilizando este teorema, se puede encontrar el ángulo desconocido al despejarlo de la fórmula.
3. Razones trigonométricas: Las razones trigonométricas como el seno, coseno y tangente, pueden ser utilizadas para calcular los ángulos de un triángulo rectángulo si se conocen las longitudes de los catetos y la hipotenusa.
4. Utilización de instrumentos de medición: En algunos casos, puede ser necesario utilizar instrumentos de medición como niveladores o inclinómetros para determinar con precisión los ángulos de un triángulo rectángulo.

Es importante recordar que calcular el ángulo de un triángulo rectángulo requiere de un análisis cuidadoso de los datos disponibles y la aplicación correcta de las técnicas matemáticas adecuadas. Es recomendable contar con un buen conocimiento de trigonometría y práctica en el uso de las fórmulas mencionadas.

Conocer el ángulo de un triángulo rectángulo es esencial en disciplinas como la arquitectura y la ingeniería, ya que garantiza estructuras seguras y bien diseñadas. Existen diferentes técnicas y herramientas para realizar estos cálculos, pero es fundamental contar con una comprensión sólida de la trigonometría y práctica en su aplicación.

Cuáles son algunos consejos útiles para calcular el ángulo de un triángulo rectángulo de manera más precisa y eficiente

Paso 1: Conoce las propiedades de un triángulo rectángulo

Antes de adentrarnos en el cálculo de los ángulos de un triángulo rectángulo, es importante comprender algunas propiedades básicas de este tipo de figura geométrica. Un triángulo rectángulo está formado por tres lados, uno de los cuales es más largo que los otros dos. Este lado se llama hipotenusa y se encuentra opuesto al ángulo recto, que mide exactamente 90 grados.

Además del ángulo recto, los otros dos ángulos son agudos, es decir, miden menos de 90 grados cada uno. Estos ángulos pueden ser conocidos como ángulo A y ángulo B, donde el ángulo A es opuesto al lado más corto (cateto) y el ángulo B es opuesto al otro lado (otro cateto).

Paso 2: Utiliza el teorema de Pitágoras

Una de las formas más sencillas de calcular los ángulos en un triángulo rectángulo es utilizando el famoso teorema de Pitágoras. Este teorema establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de la longitud de los catetos. Matemáticamente, esto se puede expresar mediante la fórmula:

c^2 = a^2 + b^2

Donde c representa la longitud de la hipotenusa, mientras que a y b representan las longitudes de los catetos.

Para calcular un ángulo específico, puedes despejar dicho ángulo de la fórmula del teorema de Pitágoras. Por ejemplo, si quieres encontrar el ángulo A, puedes utilizar la siguiente fórmula:

sen(A) = a / c

Paso 3: Usa las razones trigonométricas

Otra forma de calcular los ángulos en un triángulo rectángulo es utilizando las razones trigonométricas. Las tres principales razones trigonométricas son: seno (sen), coseno (cos) y tangente (tan).

Si conoces las longitudes de dos de los lados de un triángulo rectángulo, puedes utilizar estas razones trigonométricas para calcular los ángulos. Por ejemplo, si tienes la longitud de la hipotenusa y la longitud del cateto adyacente al ángulo que deseas hallar, puedes usar el coseno:

cos(A) = cateto adyacente / hipotenusa

Recuerda que estas razones trigonométricas solo pueden ser aplicadas en triángulos rectángulos y son especialmente útiles para determinar ángulos cuando se conocen las longitudes de los lados.

Paso 4: Utiliza la calculadora o una app especializada

Si buscas una manera más rápida y precisa de calcular los ángulos de un triángulo rectángulo, siempre puedes recurrir a herramientas digitales como una calculadora o una aplicación especializada. Estas herramientas suelen tener funciones específicas para resolver problemas de trigonometría y pueden ahorrarte tiempo y esfuerzo en los cálculos.

Existen varias formas de calcular los ángulos de un triángulo rectángulo. Puedes utilizar el teorema de Pitágoras, las razones trigonométricas o incluso herramientas digitales para obtener resultados precisos. ¡Recuerda practicar y familiarizarte con estas técnicas para convertirte en un experto en el cálculo de ángulos!

Dónde puedo encontrar herramientas o calculadoras en línea que me ayuden a realizar estos cálculos

Si estás buscando herramientas o calculadoras en línea para ayudarte a calcular el ángulo de un triángulo rectángulo, estás de suerte. Existen varias opciones disponibles que pueden facilitar este proceso y proporcionarte resultados precisos de manera rápida y sencilla.

1. Calculadora de ángulos de triángulos rectángulos

Una opción popular es utilizar una calculadora específica para calcular los ángulos de un triángulo rectángulo. Estas calculadoras suelen ser fáciles de usar y requieren que ingreses algunas medidas relacionadas con el triángulo, como la longitud de los lados o las medidas de los ángulos conocidos.

Calculadora de ángulos de triángulos rectángulos

2. Software y aplicaciones móviles

Otra opción es utilizar software especializado o aplicaciones móviles que incluyan herramientas de cálculo de ángulos de triángulos rectángulos. Estas herramientas suelen ofrecer mayor flexibilidad y funcionalidad que las calculadoras en línea, permitiéndote realizar otros cálculos y obtener información adicional sobre los triángulos rectángulos.

Algunas aplicaciones populares incluyen:

• Triángulos Rectángulos App: Disponible tanto en iOS como en Android, esta aplicación ofrece una interfaz intuitiva y fácil de usar para calcular los ángulos de un triángulo rectángulo.
• Geogebra: Esta aplicación gratuita proporciona una amplia gama de herramientas geométricas, incluyendo cálculos de triángulos rectángulos y ángulos.

3. Software de diseño gráfico o CAD

Si estás trabajando en un proyecto de diseño gráfico o ingeniería que requiere cálculos precisos de los ángulos de un triángulo rectángulo, es posible que desees utilizar software especializado de diseño gráfico o CAD (diseño asistido por computadora). Estos programas suelen ofrecer herramientas avanzadas para el dibujo y la medición de figuras geométricas, lo que facilita el cálculo de los ángulos de un triángulo rectángulo.

Algunos ejemplos de software de diseño gráfico o CAD incluyen:

1. AutoCAD: Uno de los programas más utilizados en diseño gráfico e ingeniería, AutoCAD ofrece una amplia gama de herramientas para el dibujo y la medición de figuras geométricas.
2. SolidWorks: Este software de CAD es conocido por sus capacidades de modelado 3D, pero también incluye herramientas para el cálculo de ángulos en triángulos rectángulos.

Si estás buscando herramientas o calculadoras en línea para calcular los ángulos de un triángulo rectángulo, hay varias opciones disponibles. Puedes utilizar calculadoras en línea específicas, descargar aplicaciones móviles con estas funcionalidades o utilizar software de diseño gráfico o CAD para obtener resultados precisos y sencillos.

Cuál es la importancia de comprender y dominar el cálculo de ángulos en triángulos rectángulos en situaciones cotidianas

Comprender y dominar el cálculo de ángulos en triángulos rectángulos es una habilidad fundamental en matemáticas que tiene una gran relevancia en diferentes situaciones cotidianas. Estos cálculos nos permiten determinar medidas precisas y resolver problemas relacionados con la geometría y las propiedades de los triángulos rectángulos.

Uno de los usos más comunes del cálculo de ángulos en triángulos rectángulos es en navegación marítima y aérea. Los pilotos y navegantes deben ser capaces de calcular el ángulo formado entre su posición y un punto de referencia fijo, como una boya o una estrella, para determinar su rumbo o su posición exacta. Este cálculo es esencial para garantizar la seguridad y la precisión en la navegación.

Otra aplicación importante se encuentra en la arquitectura y la ingeniería civil. Los arquitectos e ingenieros utilizan el cálculo de ángulos en triángulos rectángulos para diseñar estructuras seguras y estables, como puentes y edificios. A través de estos cálculos, pueden determinar la inclinación exacta de las rampas, escaleras o pendientes para garantizar la accesibilidad y la seguridad de las personas.

En el ámbito de la física, el cálculo de ángulos en triángulos rectángulos es esencial para entender fenómenos como la caída libre de objetos o el movimiento de proyectiles. Al conocer los ángulos de lanzamiento y la trayectoria de los objetos, los físicos pueden predecir con precisión la altura máxima, el tiempo de vuelo y la distancia recorrida por un objeto en movimiento.

En el campo de las tecnologías de la información y la comunicación, el cálculo de ángulos en triángulos rectángulos es fundamental para desarrollar aplicaciones y software que utilizan sensores de movimiento. Estos sensores miden los ángulos formados entre los ejes de referencia y la posición del objeto o individuo. De esta manera, se pueden detectar gestos, movimientos o inclinaciones, lo que permite controlar dispositivos electrónicos o realizar acciones específicas.

Comprender y dominar el cálculo de ángulos en triángulos rectángulos es importante no solo en el ámbito académico y matemático, sino también en situaciones cotidianas como la navegación, la arquitectura, la física y las tecnologías de la información y la comunicación. Estos cálculos nos permiten tomar decisiones precisas, garantizar la seguridad y diseñar estructuras eficientes en diferentes áreas de nuestra vida diaria.

Preguntas frecuentes (FAQ)

1. ¿Cómo se calcula el ángulo de un triángulo rectángulo?

Se puede calcular utilizando la función trigonométrica inversa, como por ejemplo la tangente o el seno inverso.

2. ¿Qué es un triángulo rectángulo?

Es un tipo de triángulo que tiene un ángulo recto, es decir, un ángulo de 90 grados.

3. ¿Es posible tener dos ángulos rectos en un triángulo rectángulo?

No, en un triángulo rectángulo solo puede haber un ángulo recto, que es de 90 grados.

4. ¿Cuál es la suma de los ángulos de un triángulo rectángulo?

La suma de los ángulos de cualquier triángulo siempre es igual a 180 grados.

5. ¿Qué diferencia hay entre el seno y la tangente de un ángulo en un triángulo rectángulo?

El seno es la razón entre el cateto opuesto y la hipotenusa, mientras que la tangente es la razón entre el cateto opuesto y el cateto adyacente.