Descubre cómo sacar el lado recto de una parábola y domina su curvatura en simples pasos

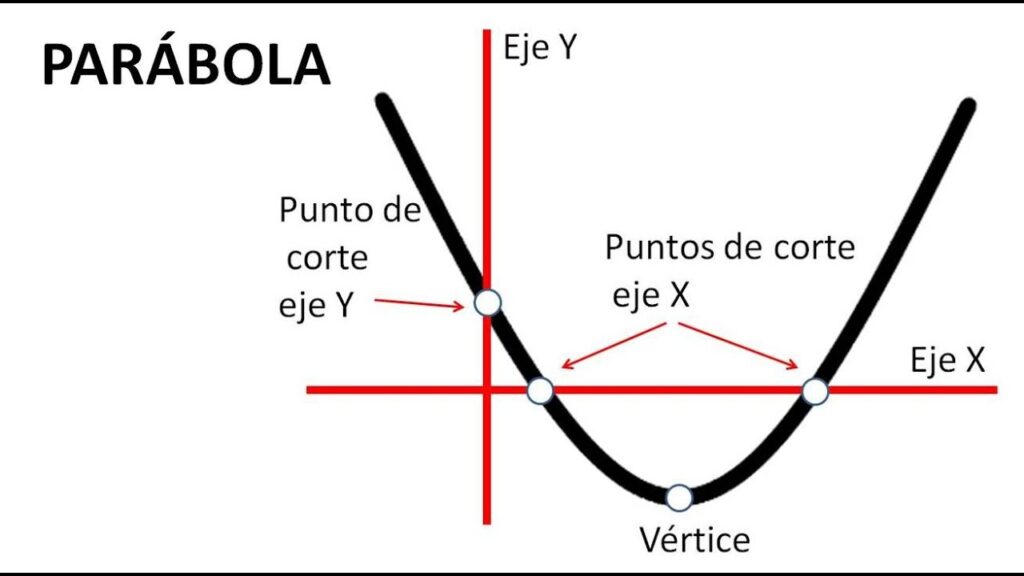
Las parábolas son uno de los conceptos fundamentales en la geometría y las matemáticas en general. Su estructura curva es ampliamente utilizada en distintas áreas como la física, la ingeniería y la arquitectura. Comprender cómo funciona esta figura geométrica y cómo sacar su lado recto puede ser de gran ayuda a la hora de resolver problemas complejos o realizar diseños precisos.

Exploraremos los mecanismos detrás de una parábola y analizaremos detenidamente cómo encontrar su lado recto. Además, aprenderemos a controlar su curvatura mediante distintos métodos y técnicas que facilitarán la resolución de problemas prácticos. Ya sea que estés estudiando matemáticas o simplemente quieras conocer más sobre este tema, te invitamos a seguir leyendo para descubrir todo sobre las parábolas y cómo sacarles el máximo provecho.

¿Qué es una parábola y cuál es su definición exacta?

Una parábola es una curva que se presenta en el plano, definida como el conjunto de puntos equidistantes de un punto fijo llamado foco y de una recta fija llamada directriz. Su forma característica es similar a la letra "U" invertida y cuenta con diversas aplicaciones en áreas como la física, la geometría y la ingeniería.

La definición exacta de una parábola puede variar dependiendo del contexto en el que se utilice. Desde una perspectiva matemática, se puede describir como la gráfica de una función cuadrática de segundo grado, representando una relación entre dos variables, generalmente llamadas x e y. En la forma algebraica, la ecuación general de una parábola tiene la forma Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0, donde A, B, C, D, E y F son constantes.

Desde una perspectiva más visual, una parábola se puede entender como la trayectoria descrita por un objeto lanzado en el aire bajo la influencia exclusiva de la gravedad. Por ejemplo, cuando se lanza una pelota hacia arriba y luego cae al suelo, su trayectoria sigue una parábola. Este tipo de parábola se conoce como parábola de trayectoria o parábola de vuelo.

En física, las leyes del movimiento de los cuerpos también involucran el concepto de parábola. La parábola es el resultado de la combinación de una velocidad constante en el eje horizontal y una aceleración vertical debido a la gravedad. El lanzamiento de un proyectil, como una bala o una flecha, sigue una parábola en su trayectoria. Este tipo de parábola se conoce como parábola de tiro parabólico.

En geometría, las propiedades y características de las parábolas son ampliamente estudiadas. Por ejemplo, cada parábola tiene un vértice, que es el punto más bajo o más alto de la curva, dependiendo de si se abre hacia arriba o hacia abajo. La distancia entre el vértice y el foco se llama distancia focal y está relacionada con la longitud focal de una parábola. La directriz de una parábola es una recta perpendicular al eje de simetría y equidistante al foco.

Una parábola es una figura geométrica que puede ser representada por una ecuación cuadrática, descrita como la gráfica de una función cuadrática o asociada a la trayectoria de un objeto bajo la influencia de la gravedad. Tiene propiedades y características únicas que pueden ser estudiadas desde diferentes perspectivas matemáticas y físicas.

¿Cuáles son las características clave de una parábola?

La parábola es una de las curvas más conocidas y estudiadas en la geometría. Sus características clave son su simetría, su fórmula general y su vértice.

En primer lugar, la simetría de una parábola es una de sus propiedades más destacadas. Una parábola tiene un eje de simetría vertical que pasa por su vértice. Esto significa que si trazamos una línea imaginaria a través de la parábola, dividiéndola en dos partes iguales, los puntos correspondientes en ambos lados de la línea tendrán la misma distancia vertical al eje de simetría.

La fórmula general de una parábola también es importante para comprender y trabajar con esta curva. La fórmula general de una parábola que se abre hacia arriba o hacia abajo se representa como:

y = ax^2 + bx + c

Donde "a", "b" y "c" son constantes y determinan la forma y posición de la parábola. El coeficiente "a" determina la concavidad de la parábola, mientras que los coeficientes "b" y "c" controlan su desplazamiento horizontal y vertical, respectivamente.

Finalmente, el vértice de la parábola es otro aspecto crucial a tener en cuenta. El vértice es el punto más bajo (en caso de que la parábola se abra hacia arriba) o el punto más alto (si la parábola se abre hacia abajo) de la curva. El vértice tiene coordenadas (h, k), donde "h" es el valor del desplazamiento horizontal y "k" es la coordenada vertical del vértice.

Domina el lado recto de una parábola

Muchas veces, al enfrentarnos a problemas relacionados con parábolas, necesitamos encontrar el lado recto de la curva. Para ello, debemos identificar el intervalo en el cual la parábola tiene una pendiente constante y, por lo tanto, es completamente recta.

Para encontrar el lado recto de una parábola, podemos utilizar conceptos como las raíces o los puntos de inflexión. Las raíces de una parábola son los valores de "x" para los cuales la ecuación de la parábola se hace cero, mientras que los puntos de inflexión son aquellos donde cambia su concavidad.

Una vez que hemos identificado estos puntos clave, podemos determinar el intervalo en el que la parábola es recta. En este intervalo, la pendiente de la parábola es constante y se puede considerar como el lado recto de la curva.

Para visualizar este lado recto, podemos trazar una línea recta que sea paralela al eje "x" y que pase por el punto medio entre las raíces de la parábola. Esta línea representará el lado recto de la curva.

Dominando la curvatura de la parábola

Por otro lado, entender y dominar la curvatura de una parábola también es fundamental para trabajar con esta curva de manera efectiva. La curvatura de una parábola puede describirse en términos de su convexidad o concavidad.

Si la parábola está abierta hacia arriba, se dice que es convexa. Esto significa que la curva se "abre" hacia arriba y tiene una forma de "U". Por otro lado, si la parábola está abierta hacia abajo, se considera cóncava. En este caso, la curva se "abre" hacia abajo y tiene una forma de "n".

Para entender mejor la curvatura de una parábola, podemos analizar el signo del coeficiente "a" en la fórmula general de la parábola. Si "a" es positivo, la parábola será convexa, mientras que si "a" es negativo, la parábola será cóncava.

Además, para determinar la dirección en la que la parábola se abre, podemos observar el coeficiente de "x^2" en la fórmula general. Si este coeficiente es positivo, la parábola se abrirá hacia arriba, y si es negativo, la parábola se abrirá hacia abajo.

Conocer las características clave de una parábola, como su simetría, su fórmula general y su vértice, nos permitirá comprender y trabajar con esta curva de manera más efectiva. Además, dominar el lado recto y la curvatura de una parábola nos ayudará a resolver problemas y aplicar conceptos relacionados con esta figura geométrica con mayor precisión.

¿Cuál es la relación entre la forma de una parábola y su ecuación?

Las parábolas son una de las curvas más comunes en las matemáticas y se encuentran en muchas aplicaciones del mundo real. Comprender la relación entre la forma de una parábola y su ecuación es fundamental para poder sacar el lado recto de una parábola y dominar su curvatura.

Para entender mejor esta relación, es importante recordar que la ecuación general de una parábola es de la forma y = ax^2 + bx + c, donde a, b y c son constantes determinadas por los valores específicos de la parábola. La variable x representa los puntos en el eje horizontal, mientras que la variable y representa los puntos en el eje vertical.

La concavidad de una parábola

La concavidad de una parábola se refiere a si la curva se abre hacia arriba o hacia abajo. Esta propiedad está determinada por el coeficiente a en la ecuación general de la parábola.

• Si a > 0, la parábola se abre hacia arriba.
• Si a < 0, la parábola se abre hacia abajo.

La concavidad afecta la forma general de la parábola y cómo se curva. Por lo tanto, entender la relación entre el coeficiente a y la concavidad es fundamental para trabajar con parábolas.

El vértice de una parábola

El vértice de una parábola es el punto más alto o más bajo de la curva, también conocido como el punto máximo o mínimo. La fórmula para encontrar las coordenadas del vértice de una parábola dada por la ecuación y = ax^2 + bx + c es:

x = -b / (2a)
y = f(x) = a(x - h)^2 + k

Donde h y k son las coordenadas del vértice.

En términos simples, el vértice de una parábola se encuentra en el punto medio del eje de simetría de la curva. Afecta tanto la posición como la forma de la parábola.

El lado recto de una parábola

El lado recto de una parábola es una línea recta que pasa por el vértice y es perpendicular al eje focal de la parábola. Esta línea tiene características especiales que lo distinguen de otros puntos en la parábola.

Para sacar el lado recto de una parábola, necesitamos conocer las coordenadas del vértice. Una vez que tenemos el vértice (h, k), podemos utilizar la fórmula del lado recto:

y = k + ((x - h)^2) / (4a)

Aquí, el valor de a determina la pendiente del lado recto. Si a > 0, el lado recto se inclina hacia la derecha, mientras que si a < 0, el lado recto se inclina hacia la izquierda. El valor de a también afecta la longitud del lado recto.

Una vez que sabemos cómo sacar el lado recto de una parábola, podemos utilizar esta información para dibujar representaciones gráficas precisas de las parábolas y comprender mejor su comportamiento.

La forma de una parábola está directamente relacionada con su ecuación, específicamente con los coeficientes a, b y c. La concavidad, el vértice y el lado recto de una parábola son propiedades importantes a tener en cuenta al trabajar con estas curvas. Al dominar estos conceptos, podrás resolver problemas relacionados con las parábolas y utilizarlas de manera efectiva en aplicaciones prácticas.

¿Cómo puedo encontrar el vértice de una parábola?

El vértice de una parábola es un punto crucial que determina su forma y posición en un plano cartesiano. En el caso de las parábolas con eje vertical, el vértice se encuentra en el punto más bajo o más alto de la curva, dependiendo de la concavidad de la misma.

Para encontrar el vértice de una parábola, primero necesitamos tener la ecuación de la misma en su forma general: y = ax^2 + bx + c. Una vez que tenemos la ecuación, podemos identificar fácilmente las coordenadas del vértice utilizando la fórmula específica de la abscisa y la ordenada del vértice.

Fórmula de la abscisa del vértice:

La abscisa del vértice, denotada como xv, se calcula utilizando la fórmula:

xv = -b / (2a)

En esta fórmula, el coeficiente a corresponde al término cuadrático de la ecuación, mientras que b es el coeficiente lineal.

Por ejemplo, si tenemos la siguiente ecuación de una parábola: y = 2x^2 - 4x + 3, podemos utilizar la fórmula de la abscisa del vértice para encontrar su valor:

xv = -(-4) / (2(2)) = 1

Entonces, la abscisa del vértice es xv = 1.

Fórmula de la ordenada del vértice:

La ordenada del vértice, denotada como yv, se puede calcular utilizando la fórmula:

yv = a(xv)^2 + b(xv) + c

En esta fórmula, utilizamos el valor obtenido para la abscisa del vértice (xv), así como los coeficientes a, b y c de la ecuación.

yv = 2(1)^2 - 4(1) + 3 = 1

Por lo tanto, la ordenada del vértice es yv = 1.

Finalmente, podemos determinar las coordenadas completas del vértice, que en este caso son (1, 1).

Para encontrar el vértice de una parábola, necesitamos conocer su ecuación en forma general. A partir de esta ecuación, podemos utilizar la fórmula de la abscisa del vértice para encontrar el valor de xv, y luego utilizar la fórmula de la ordenada del vértice para obtener el valor de yv. Estos valores representan las coordenadas del vértice en el plano cartesiano, lo cual nos permite comprender mejor la forma y posición de la parábola.

¿Cuál es la fórmula para el eje de simetría de una parábola?

La fórmula para encontrar el eje de simetría de una parábola está relacionada con la ecuación general de una parábola, que es de la forma y = ax^2 + bx + c. Para determinar el eje de simetría, primero debemos identificar los coeficientes a, b y c en la ecuación.

Una vez que hemos identificado los coeficientes, podemos utilizar la fórmula del eje de simetría, que es x = -b / (2a). Esta fórmula nos dará el valor de x que representa el eje vertical de simetría de la parábola.

Para ilustrar cómo funciona esta fórmula, consideremos un ejemplo. Supongamos que tenemos la siguiente ecuación de parábola: y = 2x^2 + 4x + 1. En este caso, podemos identificar que a = 2, b = 4 y c = 1.

Aplicando la fórmula del eje de simetría, obtenemos:

x = -4 / (2 * 2) = -4 / 4 = -1

Por lo tanto, el eje de simetría de esta parábola se encuentra en x = -1. Esto significa que la parábola es simétrica respecto al punto (-1, y), donde podemos sustituir cualquier valor de y.

El eje de simetría es una línea recta perpendicular al eje x que divide la parábola en dos partes iguales. Esta propiedad de simetría es muy útil para trazar la gráfica de una parábola y comprender su comportamiento.

Es importante tener en cuenta que el eje de simetría siempre pasa por el vértice de la parábola, que es el punto más bajo (o más alto) de la curva. El conocimiento del eje de simetría nos proporciona información valiosa sobre la forma y la dirección de la parábola.

La fórmula para encontrar el eje de simetría de una parábola es x = -b / (2a). Al determinar el eje de simetría, podemos entender mejor la forma y la curvatura de la parábola, lo que nos permite hacer análisis más precisos y trazar gráficas con mayor facilidad.

¿Cuáles son los pasos para graficar una parábola en el plano cartesiano?

Para graficar una parábola en el plano cartesiano, es importante entender su forma básica y los pasos necesarios para trazarla de manera precisa. Aunque pueda parecer intimidante al principio, una vez que domines estos pasos simples, podrás sacar el máximo provecho de esta poderosa curva matemática.

Paso 1: Identificar la ecuación de la parábola

El primer paso para graficar una parábola es identificar su ecuación. La forma general de una ecuación de segundo grado (parábola) es y = ax^2 + bx + c, donde a, b y c son constantes.

Es importante tener en cuenta que el valor de a determina si la parábola se abre hacia arriba (a > 0) o hacia abajo (a < 0). Además, el signo de b afectará la posición del eje de simetría de la parábola.

Paso 2: Determinar el vértice de la parábola

El próximo paso es calcular el vértice de la parábola, que es el punto más alto (o más bajo) de la curva. Para esto, podemos utilizar la fórmula del vértice:
V = (-b/2a, f(-b/2a))

Donde V representa el vértice de la parábola, b y a son las constantes de la ecuación. Para encontrar f(-b/2a), simplemente reemplaza x por -b/2a en la ecuación original.

Paso 3: Encontrar los puntos críticos

Los puntos críticos son aquellos en los que la pendiente de la parábola es igual a cero. Estos puntos se encuentran resolviendo la derivada de la ecuación con respecto a x. Estos puntos críticos nos ayudan a definir la dirección de la concavidad de la parábola y si alcanza un máximo o mínimo.

Paso 4: Trazar el eje de simetría

El siguiente paso es trazar el eje de simetría de la parábola, que pasa por el vértice y divide la curva en dos partes iguales. El eje de simetría tiene una fórmula general de x = -b/2a.

Paso 5: Calcular otros puntos

Una vez que hemos encontrado el vértice, los puntos críticos y el eje de simetría, podemos calcular fácilmente otros puntos para tener una mejor idea de cómo se ve la parábola. Puedes elegir varios valores para x y usar la ecuación de la parábola para encontrar las correspondientes y.

Paso 6: Graficar la parábola

Con los puntos obtenidos en el paso anterior, puedes comenzar a trazar la parábola en el plano cartesiano. Utiliza una regla o un compás para conectar los puntos y asegurarte de que la curva sea suave y se ajuste correctamente.

Recuerda que estos pasos son una guía básica para ayudarte a graficar una parábola, pero es posible que encuentres variaciones y casos especiales según el tipo de ecuación y sus coeficientes. Siempre verifica tus resultados y no dudes en buscar más información o pedir ayuda si es necesario.

Ahora que conoces los pasos para graficar una parábola en el plano cartesiano, puedes explorar y dominar esta poderosa curvatura matemática. Recuerda practicar y experimentar con diferentes ecuaciones para mejorar tus habilidades gráficas y comprensión de las parábolas. ¡Diviértete explorando este fascinante mundo matemático!

¿Cómo puedo determinar si una parábola abre hacia arriba o hacia abajo?

Para determinar si una parábola abre hacia arriba o hacia abajo, debemos tomar en cuenta el coeficiente principal 'a' de la ecuación cuadrática representativa. La forma general de una ecuación cuadrática es:

y = ax^2 + bx + c

• Si el coeficiente 'a' es positivo, la parábola abrirá hacia arriba.
• Si el coeficiente 'a' es negativo, la parábola abrirá hacia abajo.

Lo importante de identificar si una parábola abre hacia arriba o hacia abajo es que nos permite conocer su concavidad y cómo se comportará a lo largo del plano cartesiano. Si una parábola abre hacia arriba, tendrá un punto mínimo y su gráfica asemejará una "U" invertida. Por otro lado, si una parábola abre hacia abajo, tendrá un punto máximo y su gráfica será similar a una "U" normal.

¿Qué podemos hacer para sacar el lado recto de una parábola?

La obtención del lado recto de una parábola puede realizarse mediante un proceso sencillo utilizando los conceptos básicos de las ecuaciones cuadráticas. Para ello, podemos seguir los siguientes pasos:

1. Identifica la ecuación de la parábola que estás analizando.
2. Determina si la parábola abre hacia arriba o hacia abajo. Esto lo puedes hacer revisando el coeficiente principal 'a'.
3. Encuentra el vértice de la parábola utilizando la fórmula:

x = -b / (2a)

Donde 'x' representa el valor de la variable independiente en el vértice y 'a' y 'b' son los coeficientes de la ecuación cuadrática.

4. Sustituye el valor obtenido en el paso anterior en la ecuación original de la parábola.
5. Resuelve la ecuación resultante para encontrar el valor correspondiente de 'y' en el punto del vértice.

Una vez que hayas realizado estos pasos, habrás encontrado el lado recto de la parábola. Recuerda que este segmento es perpendicular al eje de simetría de la parábola y su longitud se determina por la distancia entre los puntos extremos del lado recto.

¿Qué papel juegan los coeficientes en la ecuación de una parábola?

Para comprender cómo sacar el lado recto de una parábola y dominar su curvatura, es fundamental entender el papel que juegan los coeficientes en la ecuación de una parábola. Estos coeficientes son los números que aparecen en la fórmula general de una parábola, que tiene la forma de y = ax^2 + bx + c.

El primer coeficiente, a, determina la concavidad de la parábola. Si a es negativo, la parábola abrirá hacia abajo, mientras que si es positivo, la parábola abrirá hacia arriba. Además, cuanto mayor sea el valor absoluto de a, más pronunciada será la curvatura de la parábola.

El segundo coeficiente, b, afecta la posición horizontal de la parábola. Controla el desplazamiento de la parábola hacia la izquierda o hacia la derecha. Si b es positivo, la parábola se desplazará hacia la izquierda, mientras que si es negativo, se desplazará hacia la derecha. El valor absoluto de b determina qué tan rápido se produce este desplazamiento.

Por último, el tercer coeficiente, c, determina la posición vertical de la parábola. Indica dónde la parábola cruza el eje y. Si c es positivo, la parábola estará por encima del eje y, mientras que si es negativo, estará por debajo del eje. El valor de c también influye en qué tan alta o baja es la parábola con respecto al origen.

Al comprender estos conceptos básicos sobre los coeficientes en la ecuación de una parábola, podrás tener un mejor control sobre su forma y posición en el plano cartesiano. Esto te permitirá manipularla según tus necesidades y obtener resultados más precisos al sacar su lado recto o dominar su curvatura.

¿Cuál es la importancia de la curvatura de una parábola en sus aplicaciones prácticas?

La curvatura de una parábola es un concepto fundamental en matemáticas y tiene una gran importancia en diversas aplicaciones prácticas. Esta curva característica de una parábola se puede observar en diversos objetos y fenómenos de la naturaleza, así como también en el diseño de estructuras arquitectónicas y en la mecánica de fluidos.

En primer lugar, entender y dominar la curvatura de una parábola nos permite analizar y predecir el comportamiento de objetos en movimiento que siguen trayectorias parabólicas. Por ejemplo, en el campo de la física, las leyes del movimiento de los proyectiles y la trayectoria de los misiles se describen mediante ecuaciones parabólicas. Comprender la curvatura de estas trayectorias es fundamental para calcular su alcance, tiempo de vuelo y otros parámetros clave.

Asimismo, en el diseño y construcción de estructuras arquitectónicas, la comprensión de la curvatura de una parábola es esencial. Este tipo de curva se puede encontrar en techos abovedados y cúpulas, donde su forma curva ayuda a distribuir uniformemente las cargas y proporciona estabilidad estructural. Además, las ventanas y las entradas de luz con forma de arco parabólico son utilizadas para maximizar la entrada de luz natural y crear espacios visualmente atractivos.

La curvatura de una parábola también es crucial en el campo de la mecánica de fluidos. Muchos diseños de canales, tuberías y conductos de flujo utilizan curvas parabólicas para controlar y dirigir el flujo de líquidos o gases de manera eficiente. Al ajustar la curva de una parábola, se puede lograr una distribución uniforme del flujo y minimizar los puntos de estancamiento o turbulencia.

Comprender la curvatura de una parábola es fundamental en muchas aplicaciones prácticas, desde el diseño arquitectónico hasta la ingeniería y la física. Esta curva característica nos permite analizar y predecir el comportamiento de objetos en movimiento, diseñar estructuras estables y controlar el flujo de líquidos y gases de manera eficiente. Dominar el lado recto de una parábola y su curvatura en simples pasos nos permitirá aprovechar al máximo su potencial en diferentes áreas de estudio y aplicación.

¿Cómo puedo calcular la longitud focal de una parábola?

Calcular la longitud focal de una parábola puede parecer un desafío complicado, pero en realidad es más sencillo de lo que parece. La longitud focal, también conocida como distancia focal, es un parámetro importante de una parábola que nos permite comprender su forma y curvatura. En este artículo, te guiaré paso a paso para que puedas sacar el lado recto de una parábola y dominar su curvatura en simples pasos.

Paso 1: Conoce la ecuación general de una parábola

Antes de poder calcular la longitud focal de una parábola, es fundamental tener claridad sobre cómo se representa una parábola matemáticamente. La ecuación general de una parábola tiene la forma:

y = ax^2 + bx + c

Donde 'a', 'b' y 'c' son constantes. El valor de 'a' determina si la parábola abre hacia arriba (cuando 'a' es positivo) o hacia abajo (cuando 'a' es negativo).

Paso 2: Identifica los coeficientes de la ecuación general

Ahora que conocemos la ecuación general de una parábola, el siguiente paso es identificar los valores de 'a', 'b' y 'c'. Estos coeficientes nos darán información sobre la forma, posición y curvatura de la parábola.

Por ejemplo, consideremos la ecuación:

y = 2x^2 + 4x + 1

En esta ecuación, 'a' = 2, 'b' = 4 y 'c' = 1.

Paso 3: Utiliza la fórmula para calcular la longitud focal

Una vez que tenemos identificados los coeficientes de la ecuación general de la parábola, podemos utilizar la siguiente fórmula para calcular la longitud focal:

f = 1 / (4a)

Donde 'f' representa la longitud focal y 'a' es el coeficiente asociado al término cuadrático. Siguiendo con el ejemplo anterior, podemos sustituir el valor de 'a' en la fórmula:

f = 1 / (4 * 2) = 1/8

Por lo tanto, la longitud focal de la parábola representada por la ecuación y = 2x^2 + 4x + 1 es igual a 1/8.

Paso 4: Verifica la posición de la parábola

Una vez que has calculado la longitud focal, es importante verificar si la parábola se abre hacia arriba o hacia abajo. Esto se puede determinar observando el valor del coeficiente 'a'. Si 'a' es positivo, la parábola se abre hacia arriba; si 'a' es negativo, la parábola se abre hacia abajo.

En nuestro ejemplo, como 'a' es positivo (2), podemos concluir que la parábola y = 2x^2 + 4x + 1 se abre hacia arriba.

Paso 5: Interpreta el resultado

Una vez que hayas calculado la longitud focal y verificado la posición de la parábola, es importante interpretar el resultado en el contexto del problema que estás resolviendo. La longitud focal nos brinda información valiosa sobre la concavidad de la parábola.

En nuestro ejemplo, la longitud focal de 1/8 indica que la parábola tiene una curvatura más pronunciada en comparación con una parábola con una longitud focal mayor. Esto significa que la parábola y = 2x^2 + 4x + 1 es relativamente más "aguda" en su forma.

Recuerda que la longitud focal es solo uno de los muchos parámetros que pueden ayudarnos a comprender las características de una parábola. Es importante considerar otros elementos como el vértice, el eje de simetría y los puntos interceptados por la parábola para tener una imagen completa.

Finalmente, dominar el cálculo de la longitud focal de una parábola te permitirá comprender mejor su forma y curvatura, lo cual es esencial en muchos campos como la física, las matemáticas y la ingeniería. ¡Sigue practicando y explorando diferentes ejemplos para fortalecer tus habilidades!

¿Qué diferencias hay entre una parábola regular y una parábola invertida?

Antes de adentrarnos en cómo sacar el lado recto de una parábola y dominar su curvatura, es importante entender las diferencias entre una parábola regular y una parábola invertida. Ambas formas son resultado de la ecuación cuadrática, pero se caracterizan por tener distintas orientaciones.

Una parábola regular tiene la forma "y = ax^2 + bx + c", donde "a" representa la concavidad de la parábola, "b" determina la posición horizontal de su vértice y "c" es el término independiente que regula la posición vertical. La concavidad de una parábola regular puede ser hacia arriba (cuando "a" es positivo) o hacia abajo (cuando "a" es negativo).

Por otro lado, una parábola invertida tiene la forma "y = -ax^2 + bx + c". Aquí, la concavidad está justamente invertida en comparación con una parábola regular. En lugar de abrir hacia arriba, la parábola invertida abre hacia abajo cuando "a" es positivo e incluso, hacia arriba cuando "a" es negativo.

¿Cómo sacar el lado recto de una parábola?

El lado recto de una parábola corresponde a la parte de la curvatura donde la pendiente es cero. Matemáticamente hablando, esto se logra igualando la derivada de la ecuación cuadrática a cero:

0 = 2ax + b

Para resolver esta ecuación, despejamos "x" y nos queda:

x = -b/2a

Este valor de "x" representa la abscisa del vértice de la parábola, que es el punto más bajo o más alto de la curva, dependiendo de si la concavidad es hacia arriba o hacia abajo.

Una vez obtenida la abscisa del vértice, podemos encontrar la ordenada correspondiente reemplazando este valor en la ecuación cuadrática original. De esta manera, obtenemos las coordenadas exactas del vértice de la parábola.

Ahora que sabemos cómo sacar el lado recto de una parábola, vamos a ver cómo dominar su curvatura.

¿Cuáles son algunas aplicaciones comunes de las parábolas en la vida cotidiana?

Las parábolas son una forma específica de gráficas que se utiliza en diversos campos, desde la física y las matemáticas hasta el diseño arquitectónico y la ingeniería. Su forma curvada se asemeja a la de un arco y esto ha llevado a su amplio uso en muchas aplicaciones prácticas.

Física:

En la física, las parábolas se utilizan para describir el movimiento de objetos en trayectorias parabólicas, como el lanzamiento de proyectiles o la trayectoria de un cuerpo celeste. Esta propiedad fundamental de las parábolas ha sido fundamental en el desarrollo de la mecánica clásica y la física moderna.

Diseño arquitectónico:

En el diseño arquitectónico, las parábolas se utilizan para crear estructuras estables con formas curvas. Por ejemplo, los arcos parabólicos se utilizan en puentes y techos para distribuir el peso de manera uniforme y crear estructuras duraderas y estéticamente agradables.

Ingeniería civil:

En la ingeniería civil, las parábolas se utilizan para diseñar canales y acueductos que permiten el flujo eficiente del agua. La forma curva de la parábola ayuda a maximizar el flujo y minimizar la resistencia, lo que garantiza un suministro de agua constante y confiable.

Orientación de antenas parabólicas:

Las antenas parabólicas se utilizan para recibir señales de radio y televisión. Su forma de parábola les permite enfocar y reflejar las ondas electromagnéticas hacia un punto focal, donde se encuentra el receptor. Esto permite una recepción de señal más fuerte y confiable.

Estas son solo algunas de las muchas aplicaciones comunes de las parábolas en la vida cotidiana. Su versatilidad y características únicas han llevado al desarrollo y avance de diversas disciplinas, y conocer cómo manejar su curvatura puede abrir nuevas puertas de comprensión y aplicación en el mundo que nos rodea.

¿Cuál es la relación entre la función cuadrática y una parábola?

La función cuadrática y la parábola están estrechamente relacionadas. De hecho, la función cuadrática es una representación algebraica de una parábola.

Una función cuadrática se define como una relación matemática entre una variable llamada "x" y su imagen o valor correspondiente llamado "y". La forma general de una función cuadrática es:

y = ax^2 + bx + c

Donde "a", "b" y "c" son constantes y "a" no puede ser igual a cero. Estas constantes determinan la posición y la forma de la parábola.

Por otro lado, una parábola es una curva simétrica que se puede describir como el conjunto de todos los puntos equidistantes a un punto fijo llamado foco (F) y una recta fija llamada directriz (d). La parábola también tiene un punto especial conocido como vértice (V), que es el punto más alto o más bajo de la curvatura dependiendo de si la parábola se abre hacia arriba o hacia abajo.

Ahora bien, teniendo en cuenta esta relación entre la función cuadrática y la parábola, podemos utilizar la función cuadrática para encontrar varios elementos clave de la parábola, tales como el vértice, los puntos de intersección con los ejes, la dirección de apertura y la concavidad.

Encontrar el vértice de una parábola utilizando la función cuadrática

Una de las aplicaciones más comunes de la función cuadrática es encontrar el vértice de una parábola. El vértice se puede encontrar utilizando la siguiente fórmula:

x = -b/2a
y = f(x)

Donde "x" y "y" representan las coordenadas del vértice, "a" y "b" son los coeficientes de la función cuadrática y "f(x)" es el valor correspondiente a la evaluación de la función cuadrática en "x".

Ahora bien, recordemos que el vértice de una parábola es el punto más alto o más bajo de la curvatura, dependiendo de si la parábola se abre hacia arriba o hacia abajo. Utilizando la fórmula anterior, podemos encontrar las coordenadas del vértice, lo cual nos proporcionará información clave sobre la posición de la parábola en el plano.

La función cuadrática y la parábola están relacionadas de manera intrínseca. La función cuadrática nos proporciona una representación algebraica de la parábola, permitiéndonos determinar varios elementos importantes de su forma y posición en el plano. Uno de estos elementos clave es el vértice, cuya ubicación se puede encontrar utilizando la función cuadrática. Al comprender esta relación y utilizar adecuadamente la función cuadrática, podremos dominar la curvatura de una parábola y sacarle provecho en diferentes contextos y aplicaciones.

¿Existen otras formas de sacar el lado recto de una parábola además de utilizar la ecuación general?

¡Absolutamente! Aunque la ecuación general es una manera muy común y efectiva de encontrar el lado recto de una parábola, hay otras metodologías que puedes utilizar para dominar su curvatura. En este artículo, te mostraremos algunos pasos prácticos y sencillos para lograrlo.

1. Utilizando el punto de vértice y la directriz

Una forma alternativa de encontrar el lado recto de una parábola es utilizando su punto de vértice y la directriz. El punto de vértice (h, k) contiene la información clave sobre la posición central de la parábola en el plano coordenado. Por otro lado, la directriz es una línea recta que está a cierta distancia del vértice y es perpendicular al eje de simetría de la parábola.

Y = a( - h)^2 + k

Para encontrar el lado recto, necesitarás identificar estos valores y aplicarlos en la fórmula de la ecuación cuadrática. Al conocer la ecuación de la parábola, podrás determinar dónde la función alcanza su máximo o mínimo. Este valor será precisamente la longitud del lado recto de la parábola.

2. Basándote en la relación entre tangente y foco

Otra técnica útil para sacar el lado recto de una parábola es entender la relación entre tangente y foco. La tangente es una línea recta que toca la superficie de la parábola en un solo punto específico, mientras que el foco es otro punto especial que no está en la parábola misma, pero está relacionado con su forma y posición.

Al dibujar una línea recta desde el punto tangente hasta el foco, se crea un triángulo rectángulo, donde uno de los lados es precisamente el lado recto de la parábola. Utilizando el teorema de Pitágoras u otras relaciones trigonométricas, podrás calcular la longitud del lado recto a partir de las coordenadas del punto tangente y el foco.

3. Aplicando el método del cálculo diferencial

Una técnica más avanzada para determinar el lado recto de una parábola implica utilizar el cálculo diferencial. Primero, deberás encontrar la función que describe la curva de la parábola y luego derivarla para obtener su primera derivada. A continuación, igualarás esa derivada a cero y resolverás la ecuación resultante para encontrar los puntos críticos donde la pendiente de la parábola es cero.

Si encuentras un punto en el que la pendiente es cero, eso significa que estás en presencia de un máximo o mínimo de la función. Al evaluar esos valores extremos en la ecuación original de la parábola, obtendrás la longitud del lado recto correspondiente a ese punto específico.

Aunque la ecuación general es ampliamente utilizada, hay diversas formas de sacar el lado recto de una parábola. Ya sea utilizando el punto de vértice y la directriz, analizando la relación entre tangente y foco, o aplicando métodos de cálculo diferencial, podrás dominar la curvatura de las parábolas en simples pasos.

Recuerda practicar cada una de estas técnicas y, si trabajas con una situación específica, asegúrate de utilizar los datos correspondientes para obtener resultados precisos. ¡Diviértete explorando el increíble mundo de las parábolas y desafiándote a ti mismo con nuevos enfoques matemáticos!

Cuáles son los errores comunes al trabajar con parábolas y cómo evitarlos

Al trabajar con parábolas, es común cometer una serie de errores que pueden dificultar el dominio de su curvatura y la determinación de su lado recto. Estos errores pueden deberse tanto a la falta de comprensión de los conceptos básicos de la parábola como a la aplicación incorrecta de fórmulas y técnicas.

Falta de comprensión del concepto de parábola

Uno de los errores más frecuentes al trabajar con parábolas es la falta de comprensión del concepto en sí. Muchas veces, se confunde la parábola con otras curvas como la elipse o la hipérbola, lo que lleva a errores en los cálculos y en la interpretación de los resultados.

Es fundamental entender que una parábola es una curva plana y simétrica que se forma al cortar un cono con un plano paralelo a uno de sus generatrices. Esta definición es crucial para comprender sus características y poder trabajar con ella de forma adecuada. Por lo tanto, es recomendable revisar los conceptos básicos de geometría y cono antes de adentrarse en el estudio de las parábolas.

Aplicación incorrecta de fórmulas y técnicas

Otro error común es la aplicación incorrecta de fórmulas y técnicas específicas para el trabajo con parábolas. Es importante recordar que existen diversas fórmulas y propiedades que permiten determinar diferentes elementos de una parábola, como su vértice, foco, directriz y ecuación general.

Es fundamental utilizar correctamente estas fórmulas y técnicas, siguiendo paso a paso el proceso de resolución. Un error en la interpretación de una fórmula o en la aplicación de una técnica puede llevar a resultados erróneos e incluso a la dificultad de reconocer si se trata de una parábola o no.

Ausencia de cálculos intermedios y verificación de resultados

Finalmente, un error frecuente al trabajar con parábolas es la ausencia de cálculos intermedios y la falta de verificación de resultados. Es importante realizar todos los cálculos necesarios, mostrando claramente cada paso realizado, para evitar confusiones y errores que puedan comprometer la correcta determinación del lado recto de una parábola.

Además, es fundamental verificar los resultados obtenidos usando diferentes enfoques o métodos alternativos. Esto ayuda a confirmar la veracidad de los resultados y a detectar posibles errores en el proceso de resolución.

Para dominar la curvatura de una parábola y determinar su lado recto es fundamental evitar los errores comunes que se cometen al trabajar con esta curva. La comprensión del concepto de parábola, la correcta aplicación de fórmulas y técnicas, así como la realización de cálculos intermedios y la verificación de resultados, son aspectos clave para alcanzar un dominio completo de las parábolas.

Preguntas frecuentes (FAQ)

1. ¿Cómo puedo determinar el lado recto de una parábola?

El lado recto de una parábola se encuentra justo en el centro de la curvatura, donde se corta con el eje vertical de simetría.

2. ¿Cuál es la fórmula para encontrar las coordenadas del vértice de una parábola?

Las coordenadas del vértice de una parábola se pueden encontrar utilizando la fórmula x = -b / 2a y sustituyendo ese valor en la ecuación de la parábola para obtener el valor de y.

3. ¿Cómo puedo determinar si una parábola se abre hacia arriba o hacia abajo?

El coeficiente a en la ecuación de la parábola determina la dirección de apertura. Si a es positivo, la parábola se abre hacia arriba; si a es negativo, se abre hacia abajo.

4. ¿Qué hago si la ecuación de la parábola no está en forma canónica?

Si la ecuación de la parábola no está en forma canónica (y = a(x-h)^2 + k), puedes utilizar técnicas de factorización o completar el cuadrado para convertirla a esa forma y así encontrar el vértice y el lado recto.

5. ¿Cuál es la relación entre el foco y el vértice de una parábola?

El foco de una parábola se encuentra siempre a una distancia igual del vértice y del lado recto de la parábola. Esta distancia se conoce como la longitud focal.