Descubre cómo se clasifican las magnitudes físicas y mejora tu comprensión de la física

La física es la ciencia que estudia las propiedades y comportamientos de la materia y la energía, así como las interacciones entre ellos. Una parte fundamental de la física es el estudio de las magnitudes físicas, que son las propiedades cuantificables de los objetos y fenómenos que se analizan en esta disciplina.

Nos centraremos en entender cómo se clasifican las magnitudes físicas. Veremos que existen diferentes tipos de magnitudes, como las escalares y las vectoriales, y también aprenderemos sobre las magnitudes fundamentales y las derivadas, así como las unidades de medida asociadas a cada una de ellas. Además, examinaremos la importancia de la precisión y exactitud en las mediciones y exploraremos algunos ejemplos concretos para comprender mejor estos conceptos.

Qué es una magnitud física y por qué es importante entenderla

Una magnitud física es una propiedad o cualidad que puede medirse y expresarse cuantitativamente. En el campo de la física, las magnitudes físicas son fundamentales para describir y comprender los fenómenos naturales y las leyes que rigen el universo.

Entender las magnitudes físicas es esencial porque nos permite describir y analizar científicamente los procesos físicos que ocurren a nuestro alrededor. Nos ayuda a realizar mediciones precisas y a comparar diferentes cantidades físicas entre sí. Además, las magnitudes físicas nos permiten establecer relaciones matemáticas y encontrar patrones en los datos que recopilamos experimentalmente.

Clasificación de las magnitudes físicas

Las magnitudes físicas pueden clasificarse de diferentes formas según sus propiedades y características. A continuación, veremos algunas de las principales categorías:

• Magnitudes escalares: Son aquellas magnitudes que se pueden describir completamente con un número real y una unidad de medida. No tienen dirección ni sentido, solo valor numérico. Ejemplos de magnitudes escalares son la masa, el tiempo, la temperatura y la densidad.
• Magnitudes vectoriales: Son aquellas magnitudes que además de tener un valor numérico, también tienen dirección y sentido. Para representarlas gráficamente se utilizan flechas. Algunos ejemplos de magnitudes vectoriales son la velocidad, la aceleración, la fuerza y el desplazamiento.
• Magnitudes fundamentales: Son las magnitudes que no pueden expresarse en función de otras magnitudes. Estas magnitudes son la base para la definición de muchas otras magnitudes en el sistema internacional. Algunos ejemplos de magnitudes fundamentales son la longitud, la masa, el tiempo y la intensidad luminosa.
• Magnitudes derivadas: Son aquellas magnitudes que se obtienen a partir de combinaciones algebraicas de magnitudes fundamentales. Por ejemplo, el área se obtiene multiplicando dos longitudes, mientras que la velocidad se calcula dividiendo el desplazamiento entre el tiempo transcurrido.

Dentro de cada una de estas categorías existen muchas magnitudes físicas específicas que nos ayudan a describir diferentes fenómenos y propiedades físicas del mundo que nos rodea. Cada magnitud tiene su propia unidad de medida y su correspondiente símbolo, lo que nos permite comunicar y comparar resultados de manera precisa y estandarizada.

Comprender las magnitudes físicas nos brinda una base sólida para entender mejor los procesos físicos que ocurren a nuestro alrededor. Nos permite medir, comparar y analizar científicamente los fenómenos naturales, establecer relaciones matemáticas y encontrar patrones en los datos recopilados. Además, clasificar las magnitudes según sus propiedades y características nos ayuda a organizar y entender mejor el vasto campo de estudio de la física.

Cuáles son las magnitudes físicas fundamentales y cuáles son las derivadas

En el estudio de la física, las magnitudes físicas son elementos clave para describir los fenómenos naturales y sus características. Estas magnitudes pueden clasificarse en dos categorías principales: magnitudes físicas fundamentales y magnitudes físicas derivadas.

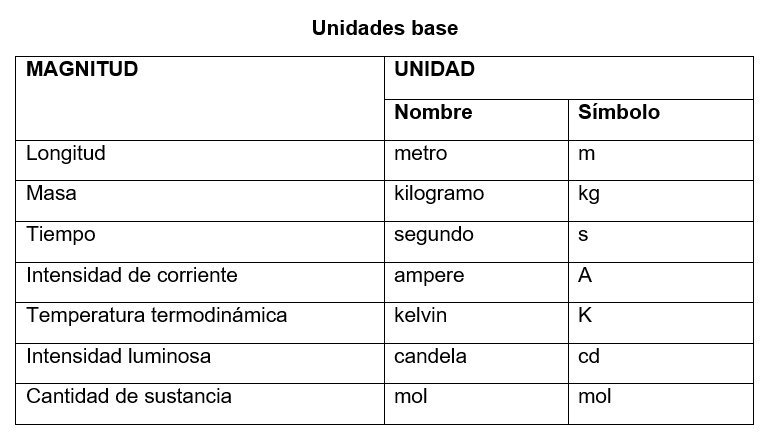
Las magnitudes físicas fundamentales son aquellas que no se pueden definir a partir de otras magnitudes. Son consideradas como las magnitudes básicas e independientes en la física. En el Sistema Internacional de Unidades (SI), hay siete magnitudes físicas fundamentales:

1. Masa: es la medida de la cantidad de materia que posee un objeto. Su unidad de medida en el SI es el kilogramo (kg).
2. Longitud: se refiere a la distancia entre dos puntos en el espacio. La unidad de medida utilizada es el metro (m).
3. Tiempo: indica la duración de un evento o sucesos. Su unidad de medida en el SI es el segundo (s).
4. Cantidad de sustancia: se relaciona con la cantidad de átomos, moléculas o partículas presentes en una sustancia. Su unidad de medida es el mol (mol).
5. Intensidad de corriente eléctrica: mide el flujo de carga eléctrica a través de un conductor. Su unidad en el SI es el amperio (A).
6. Temperatura termodinámica: indica la medida del nivel de calor o frío de un cuerpo. Su unidad en el SI es el kelvin (K).
7. Intensidad luminosa: se relaciona con la cantidad de luz emitida por una fuente luminosa. Su unidad de medida es la candela (cd).

Por otro lado, las magnitudes físicas derivadas son aquellas que se obtienen a partir de combinaciones algebraicas de las magnitudes fundamentales.

Algunos ejemplos de magnitudes físicas derivadas son:

• Velocidad: es la razón de cambio de la posición de un objeto en relación al tiempo. Se calcula dividiendo la longitud recorrida por el tiempo empleado.
• Aceleración: muestra cómo cambia la velocidad de un objeto con respecto al tiempo.
• Fuerza: se define como cualquier acción capaz de modificar el estado de movimiento o de reposo de un objeto.
• Energía: mide la capacidad de un sistema para realizar trabajo.
• Potencia: representa la tasa de transferencia de energía.

Estas son solo algunas de las muchas magnitudes físicas derivadas que existen en el estudio de la física. Comprender la clasificación de las magnitudes físicas es esencial para tener una base sólida en esta disciplina y poder aplicar correctamente los principios y leyes que rigen el mundo natural.

Cómo se clasifican las magnitudes físicas según su naturaleza

Las magnitudes físicas son todas aquellas propiedades que pueden medirse y cuantificarse en el mundo físico. Estas magnitudes se clasifican según su naturaleza, es decir, de acuerdo a la propiedad física que están representando.

Magnitudes escalares

Las magnitudes escalares son aquellas que se describen completamente con un número y una unidad. No tienen dirección ni sentido. Algunos ejemplos de magnitudes escalares son: masa, temperatura, tiempo, densidad, presión, energía, entre otras.

Magnitudes vectoriales

Por otro lado, las magnitudes vectoriales son aquellas que además de tener valor numérico y unidad, también requieren de una dirección y un sentido para ser completamente descritas. Un ejemplo claro de magnitud vectorial es la velocidad. Para especificar la velocidad de un objeto, necesitamos conocer tanto su magnitud (la velocidad en sí) como su dirección (hacia dónde se dirige) y su sentido (si va hacia adelante, hacia atrás, a la izquierda, a la derecha).

Dentro de las magnitudes vectoriales también podemos encontrar otras propiedades físicas como la aceleración, la fuerza, el desplazamiento, el momento lineal, entre otras.

Magnitudes fundamentales y derivadas

Otra forma de clasificar las magnitudes físicas es según si son fundamentales o derivadas. Las magnitudes fundamentales son aquellas que no pueden ser expresadas en función de ninguna otra magnitud. En cambio, las magnitudes derivadas son aquellas que pueden obtenerse a partir de la combinación de magnitudes fundamentales.

En el Sistema Internacional de Unidades (SI), existen siete magnitudes fundamentales: longitud, masa, tiempo, intensidad de corriente eléctrica, temperatura absoluta, cantidad de sustancia e intensidad luminosa. A partir de estas magnitudes fundamentales se definen todas las demás.

Magnitudes directamente proporcionales e inversamente proporcionales

Además de la clasificación anterior, también podemos hablar de la relación entre magnitudes físicas. Hay magnitudes que guardan una relación de proporcionalidad directa, es decir, si una aumenta, la otra también lo hace en la misma proporción. Por ejemplo, la fuerza aplicada sobre un objeto y su aceleración están directamente relacionadas según la segunda ley de Newton.

Por otro lado, hay magnitudes que guardan una relación de proporcionalidad inversa, es decir, si una aumenta, la otra disminuye en la misma proporción. Un ejemplo es la relación entre el periodo y la frecuencia de una onda: a mayor frecuencia, menor periodo y viceversa.

Las magnitudes físicas se clasifican según su naturaleza (escalares o vectoriales), si son fundamentales o derivadas, y si guardan una relación de proporcionalidad directa o inversa. Comprender estas clasificaciones es fundamental para mejorar nuestra comprensión de la física y facilitar nuestros cálculos y análisis en este campo.

Cuáles son las magnitudes físicas escalares y cuáles son vectoriales

En el campo de la física, existen dos tipos principales de magnitudes físicas: las escalares y las vectoriales. Ambos tipos son fundamentales para comprender y describir los fenómenos físicos que nos rodean.

Magnitudes físicas escalares

Las magnitudes físicas escalares son aquellas que solo requieren una cantidad numérica para describir completamente su valor. Estas magnitudes no tienen dirección ni sentido, solo indican una cantidad o intensidad. Algunos ejemplos comunes de magnitudes físicas escalares incluyen la masa, la temperatura, el tiempo, la energía y la velocidad escalar.

Cuando se trabaja con magnitudes físicas escalares, se pueden realizar operaciones matemáticas básicas como sumar, restar, multiplicar y dividir. El resultado final será simplemente un número sin ninguna dirección asociada.

Magnitudes físicas vectoriales

Por otro lado, las magnitudes físicas vectoriales son aquellas que tienen tanto magnitud como dirección. Esto significa que para describir completamente una magnitud física vectorial, se deben proporcionar tanto un número como una dirección específica. Las magnitudes vectoriales son representadas por flechas en diagramas, donde la longitud de la flecha representa la magnitud y la dirección indica la dirección del vector.

Ejemplos comunes de magnitudes físicas vectoriales incluyen la fuerza, la velocidad, el desplazamiento, la aceleración y el momento lineal. Cada una de estas magnitudes tiene una cantidad (magnitud) y una dirección específica asociada.

Diferencias entre magnitudes físicas escalares y vectoriales

La principal diferencia entre las magnitudes físicas escalares y vectoriales radica en su representación y en cómo se manipulan matemáticamente.

Las magnitudes físicas escalares solo requieren un valor numérico y no tienen dirección asociada. Por lo tanto, cuando se realizan operaciones matemáticas con estas magnitudes, se pueden utilizar reglas simples de aritmética para obtener un resultado.

En cambio, las magnitudes físicas vectoriales deben tener tanto una magnitud como una dirección. Para sumar o restar magnitudes físicas vectoriales, se utiliza la regla del paralelogramo o la regla del triángulo, dependiendo del caso. Estas reglas permiten combinar vectores teniendo en cuenta tanto su magnitud como su dirección.

Otra diferencia importante es que las magnitudes físicas vectoriales también pueden tener componentes, que indican la contribución de cada dirección en un sistema de coordenadas específico.

Las magnitudes físicas escalares y vectoriales son fundamentales en la física para describir y comprender los fenómenos naturales. Las magnitudes físicas escalares solo requieren un valor numérico, mientras que las magnitudes físicas vectoriales tienen tanto una magnitud como una dirección asociada.

Al tener una comprensión clara de la diferencia entre estos dos tipos de magnitudes físicas, podemos abordar de manera más precisa y efectiva la resolución de problemas físicos y analizar los diversos aspectos del mundo natural desde una perspectiva científica.

Qué diferencia hay entre magnitudes escalares y vectoriales

En el campo de la física, las magnitudes son variables cuantitativas que se utilizan para describir diferentes aspectos del mundo que nos rodea. Existen dos tipos principales de magnitudes: escalares y vectoriales.

Magnitudes escalares

Las magnitudes escalares son aquellas que pueden ser completamente descritas por un número y una unidad de medida. Esto significa que solo tienen una componente numérica y no están asociadas con ninguna dirección específica en el espacio.

Algunos ejemplos comunes de magnitudes escalares incluyen la masa, la temperatura, la densidad, el volumen y el tiempo. Estas magnitudes se representan mediante un número y una unidad de medida, como kilogramos (kg) para la masa o grados Celsius (°C) para la temperatura.

En muchos casos, las operaciones matemáticas que se realizan con magnitudes escalares son simples, ya que solo se requiere tener en cuenta la cantidad numérica y la unidad de medida. Por ejemplo, si tienes dos masas, digamos 5 kg y 3 kg, simplemente puedes sumar los números para obtener su suma total de 8 kg.

Magnitudes vectoriales

A diferencia de las magnitudes escalares, las magnitudes vectoriales tienen tanto una componente numérica como una dirección en el espacio. Esto significa que no solo se tiene en cuenta el valor de la magnitud, sino también dónde se encuentra en relación con un punto de referencia.

Ejemplos de magnitudes vectoriales son la velocidad, la aceleración, la fuerza, el desplazamiento y el momento. Estas magnitudes se representan utilizando una cantidad numérica, una unidad de medida y una indicación de dirección, como metros por segundo (m/s) hacia el este para la velocidad.

Las operaciones matemáticas con magnitudes vectoriales son más complejas que en el caso de las magnitudes escalares. Además de sumar o restar los valores numéricos, también es necesario considerar las direcciones de las magnitudes. Por ejemplo, si tienes dos fuerzas de 5 N hacia el norte y 3 N hacia el este, necesitarás combinar tanto los valores numéricos como las direcciones para obtener el resultado final.

La representación gráfica de las magnitudes vectoriales se realiza mediante flechas que indican la dirección y la magnitud de la cantidad representada. Estas flechas se conocen como vectores y pueden variar en longitud según la magnitud.

La diferencia fundamental entre las magnitudes escalares y vectoriales radica en que las primeras solo tienen una componente numérica, mientras que las segundas también incluyen una dirección en el espacio. Al comprender esta distinción, podemos analizar y resolver problemas físicos de manera más precisa y completa.

Cómo se representan las magnitudes físicas con unidades de medida

Para poder comprender y trabajar con las magnitudes físicas, es fundamental entender cómo se representan a través de unidades de medida. Las unidades permiten cuantificar y comparar las diferentes magnitudes presentes en el estudio de la física.

En general, existen dos tipos de magnitudes físicas: escalares y vectoriales. Las magnitudes escalares son aquellas que únicamente poseen una cantidad numérica y una unidad de medida. Por ejemplo, la longitud, masa, tiempo y temperatura son magnitudes escalares.

Por otro lado, las magnitudes vectoriales son aquellas que además de tener una cantidad numérica y una unidad de medida, también requieren de una dirección y un sentido para ser completamente especificadas. Algunos ejemplos de magnitudes vectoriales son la velocidad, la aceleración, la fuerza y el desplazamiento.

Unidades de medida

Las unidades de medida son los patrones definidos de manera convencional para representar las magnitudes físicas. Estas unidades están establecidas por sistemas de medición como el Sistema Internacional de Unidades (SI), que es el sistema más utilizado a nivel mundial.

El SI utiliza siete unidades base para representar las principales magnitudes físicas: metro (m) para la longitud, kilogramo (kg) para la masa, segundo (s) para el tiempo, kelvin (K) para la temperatura, amperio (A) para la corriente eléctrica, mol (mol) para la cantidad de sustancia y candela (cd) para la intensidad luminosa.

A partir de estas unidades base, se derivan otras unidades mediante combinaciones algebraicas o conversiones específicas. Por ejemplo, el centímetro (cm) es una unidad derivada del metro, siendo igual a 0.01 metros. Además, existen prefijos que permiten expresar múltiplos o submúltiplos de las unidades base, como el kilo (k) para mil, mega (M) para millones y mili (m) para milésimas.

Es importante destacar que algunas magnitudes físicas tienen unidades específicas que no forman parte del SI, pero que se utilizan en casos particulares. Por ejemplo, la presión se mide en pascales (Pa), la energía en julios (J) y la frecuencia en hertz (Hz).

Sistema de unidades coherentes

Para realizar cálculos y mediciones precisas, se utiliza el concepto de sistema de unidades coherentes. Este sistema consiste en utilizar un conjunto de unidades base y derivadas relacionadas entre sí mediante ecuaciones adimensionales o con exponentes enteros.

En un sistema de unidades coherentes, todas las ecuaciones físicas deben ser consistentes y no presentar discrepancias. Esto permite que los resultados obtenidos sean confiables y comparables entre diferentes experimentos o trabajos científicos.

• Por ejemplo:
• La fórmula de la velocidad promedio se expresa como:
• v = Δx / Δt
• Donde v representa la velocidad promedio, Δx el cambio en posición y Δt el cambio en tiempo.
• Si utilizamos el Sistema Internacional de Unidades, entonces Δx se medirá en metros (m) y Δt en segundos (s), lo que permitirá obtener la velocidad promedio en metros por segundo (m/s).

Las magnitudes físicas se representan a través de unidades de medida, ya sean escalares o vectoriales, y estas unidades están establecidas por sistemas de medición. El uso de un sistema de unidades coherentes asegura la consistencia y precisión de los cálculos y mediciones realizadas en el ámbito de la física.

Cuáles son los prefijos más comunes utilizados en el Sistema Internacional de Unidades (SI)

En el Sistema Internacional de Unidades (SI), se utilizan prefijos para expresar múltiplos y submúltiplos de las unidades. Estos prefijos son esenciales para poder trabajar con magnitudes en diferentes escalas, ya que nos permiten expresar valores más grandes o más pequeños de manera más conveniente.

Existen varios prefijos, pero hay algunos que son más comunes y ampliamente utilizados en la física. A continuación, te mencionaré los prefijos más comunes y algunos ejemplos de cómo se utilizan:

- Kilo (k):

Este prefijo se utiliza cuando queremos expresar un valor mil veces mayor que la unidad básica. Por ejemplo, si hablamos de kilogramo (kg), estamos hablando de 1000 gramos. Otro ejemplo común es el kilómetro (km), que equivale a 1000 metros.

- Mega (M):

El prefijo "Mega" se utiliza cuando queremos expresar un valor un millón de veces mayor que la unidad básica. Por ejemplo, si hablamos de megavatio (MW), estamos hablando de un millón de vatios. Este prefijo también se utiliza mucho en el almacenamiento de datos, donde un megabyte (MB) equivale a un millón de bytes.

- Giga (G):

El prefijo "Giga" se utiliza para expresar un valor mil millones de veces mayor que la unidad básica. Por ejemplo, un gigahertz (GHz) es igual a mil millones de hertzios. También se utiliza en el almacenamiento de datos, donde un gigabyte (GB) es igual a mil millones de bytes.

- Micro (µ):

Este prefijo se utiliza para expresar un valor un millón de veces menor que la unidad básica. Por ejemplo, un microsegundo (µs) equivale a una millonésima parte de un segundo. Otra aplicación común es el microgramo (µg), que es una millonésima parte de un gramo.

- Nano (n):

El prefijo "Nano" se utiliza cuando queremos expresar un valor mil millones de veces menor que la unidad básica. Por ejemplo, un nanosegundo (ns) es igual a una milmillonésima parte de un segundo. En la electrónica, es común utilizar este prefijo para indicar la escala de los transistores, donde un nanómetro (nm) es igual a una milmillonésima parte de un metro.

- Pico (p):

Este prefijo se utiliza para expresar un valor mil billones de veces menor que la unidad básica. Por ejemplo, un picosegundo (ps) equivale a una milbillonésima parte de un segundo. Es comúnmente utilizado en la física de partículas y en la tecnología de semiconductores.

Estos son solo algunos de los prefijos más comunes utilizados en el Sistema Internacional de Unidades. A través de su uso, podemos expresar magnitudes físicas en diferentes escalas de manera más conveniente y comprensible. Es importante familiarizarse con estos prefijos para poder interpretar y manipular las unidades correctamente en el estudio de la física.

Cuál es la importancia de tener una unidad de medida estándar para cada magnitud física

La importancia de tener una unidad de medida estándar para cada magnitud física es fundamental en el estudio y comprensión de la física. La elección de una unidad de medida adecuada garantiza la consistencia y la comparabilidad de los resultados obtenidos en diferentes experimentos y mediciones.

En la física, las magnitudes se clasifican en base a sus propiedades y características. En este sentido, el Sistema Internacional de Unidades (SI) establece las unidades estándar para cada magnitud, lo que permite una comunicación clara y precisa entre los científicos de todo el mundo.

El uso de unidades estándar facilita la interpretación de los resultados y la realización de cálculos matemáticos, ya que todos los valores se expresan en una misma escala. Además, proporciona una base sólida para el desarrollo de teorías y leyes físicas, permitiendo establecer relaciones cuantitativas entre diferentes magnitudes.

Un ejemplo destacado de la importancia de las unidades estándar es la medición del tiempo. En el pasado, cada cultura tenía su propio sistema de medición del tiempo, lo que dificultaba la comparación y el intercambio de datos. Sin embargo, con la adopción del segundo como unidad estándar de tiempo en el SI, se logró una universalización que posibilitó importantes avances en la ciencia y la tecnología.

Otro ejemplo es la medición de la longitud. Antes de la adopción del metro como unidad estándar de longitud, cada país tenía su propia definición de esta magnitud. Esto generaba mucha confusión y problemas al tratar de realizar mediciones precisas. Con la implementación del metro como unidad estándar, se logró la uniformidad y la comparabilidad de las mediciones de longitud en todo el mundo.

Tener una unidad de medida estándar para cada magnitud física es esencial para mejorar nuestra comprensión de la física. Nos permite establecer una base sólida para la realización y el análisis de experimentos, así como para el desarrollo de teorías científicas. Además, facilita la comunicación entre los científicos y promueve el intercambio de información a nivel mundial.

Cómo se pueden convertir unidades de medida de una magnitud física a otra

Para convertir unidades de medida de una magnitud física a otra, es importante comprender las relaciones entre las diferentes magnitudes y cómo se relacionan a través de factores de conversión. Las conversiones de unidades son comunes en campos como la física, la ingeniería y muchas otras disciplinas científicas.

En primer lugar, es fundamental conocer las equivalencias entre las unidades de medida. Por ejemplo, para convertir metros a kilómetros, debemos recordar que 1 kilómetro equivale a 1000 metros. Esta relación nos permite establecer un factor de conversión directo. Si tenemos 2000 metros y queremos saber la cantidad equivalente en kilómetros, simplemente dividimos 2000 entre 1000, lo que nos dará 2 kilómetros.

Sin embargo, no todas las conversiones son tan sencillas. En algunos casos, necesitamos utilizar múltiples factores de conversión para llegar a la unidad deseada. Por ejemplo, si queremos convertir los segundos a horas, debemos tener en cuenta que hay 60 segundos en un minuto y 60 minutos en una hora. Por lo tanto, podemos utilizar un factor de conversión en cascada: multiplicamos el número de segundos por 1 minuto / 60 segundos y luego multiplicamos por 1 hora / 60 minutos. Este proceso nos dará la cantidad equivalente en horas.

Es importante destacar que cuando realizamos conversiones de unidades, también debemos tener en cuenta los dígitos significativos y la precisión de los valores. Si redondeamos demasiado pronto durante el proceso de conversión, podemos introducir errores significativos en nuestros cálculos. Es recomendable realizar las conversiones al final del proceso de cálculo y conservar valores no redondeados hasta que sea necesario presentar los resultados finales.

Además de las conversiones directas, también hay casos en los que necesitamos utilizar constantes físicas para realizar las conversiones. Por ejemplo, al convertir energía de joules a calorías, utilizamos la constante de conversión 1 cal = 4.184 J. Esto nos permite establecer una relación precisa entre las dos magnitudes.

Para convertir unidades de medida de una magnitud física a otra, es fundamental conocer las equivalencias entre las unidades y utilizar factores de conversión adecuados. También debemos tener en cuenta los dígitos significativos y la precisión de los resultados. Con práctica y familiaridad con los conceptos básicos de la física, podremos dominar las conversiones de unidades y mejorar nuestra comprensión de las magnitudes físicas.

Qué es la precisión y exactitud al medir magnitudes físicas

La precisión y exactitud son dos conceptos fundamentales al medir magnitudes físicas. Ambos términos se utilizan para describir la confiabilidad de los resultados obtenidos a través de mediciones. Sin embargo, es importante tener en cuenta que no son sinónimos y tienen significados ligeramente diferentes.

Precisión

La precisión se refiere a cómo cercanos están los valores medidos entre sí cuando se realizan múltiples mediciones del mismo fenómeno. En otras palabras, la precisión indica qué tan repetibles son los resultados obtenidos. Si las mediciones son consistentes y cercanas entre sí, se considera que la técnica utilizada es precisa.

Para ilustrar esto, imagine que está midiendo la longitud de una varilla utilizando un calibrador. Si realiza varias mediciones y obtiene resultados que difieren solo ligeramente entre sí, eso indicaría una alta precisión en sus mediciones.

Es importante destacar que la precisión no garantiza la exactitud. Incluso si las mediciones son precisas, pueden estar alejadas del valor verdadero o aceptado. Esto puede ser causado por errores sistemáticos en la técnica de medición o por cualquier otro factor que afecte consistentemente los resultados.

Exactitud

La exactitud, por otro lado, se refiere a cuán cercano está el valor medido al valor verdadero o aceptado. Indica qué tan cerca está el resultado obtenido del valor "correcto". Un resultado exacto mostraría que el error entre el valor medido y el valor verdadero es pequeño.

Usando el ejemplo anterior de la medida de la longitud de una varilla, si sus mediciones se acercan al valor verdadero o aceptado, entonces se considera que ha obtenido resultados precisos.

Es importante tener en cuenta que puede haber casos en los que las mediciones sean exactas pero no precisas. Esto significa que los valores medidos pueden estar alejados unos de otros pero cercanos al valor verdadero. Por ejemplo, si mide la longitud de una varilla varias veces y obtiene valores que difieren entre sí, pero están muy cerca del valor verdadero, entonces sus mediciones son exactas pero no precisas.

La precisión se refiere a la repetibilidad de las mediciones, mientras que la exactitud se refiere a qué tan cerca está el resultado del valor verdadero. Ambos términos son importantes para evaluar la calidad de las mediciones y mejorar nuestra comprensión de la física.

Cómo se puede usar la notación científica para expresar magnitudes físicas

La notación científica es una forma de expresar las magnitudes físicas de manera más conveniente y comprensible. Es ampliamente utilizada en la física debido a la gran variedad de magnitudes que se manejan, desde partículas subatómicas hasta distancias astronómicas.

En la notación científica, una magnitud física se expresa en la forma de un número multiplicado por una potencia de 10. Por ejemplo, la velocidad de la luz en el vacío se puede escribir como 3 x 10^8 metros por segundo. Esta notación nos permite simplificar números extremadamente grandes o pequeños y hacerlos más manejables.

La potencia de 10 en la notación científica indica cuántos lugares debe moverse la coma decimal para obtener el valor numérico completo. En el ejemplo anterior, al mover la coma tres lugares hacia la derecha, obtenemos 300,000,000, que es el valor completo de la velocidad de la luz en metros por segundo.

Además de simplificar los números, la notación científica también permite comparar magnitudes físicas de manera más sencilla. Por ejemplo, si queremos comparar el diámetro de un átomo con el tamaño de la Tierra, podemos escribir el diámetro del átomo como 1 x 10^-10 metros y el diámetro de la Tierra como 1 x 10^7 metros. Al comparar las potencias de 10, nos damos cuenta de que el tamaño del átomo es aproximadamente 100 millones de veces más pequeño que el tamaño de la Tierra.

La notación científica es una herramienta invaluable en la física para expresar magnitudes físicas de manera más conveniente y comprensible. Nos permite simplificar números grandes o pequeños, así como comparar magnitudes de manera más sencilla. Si deseas mejorar tu comprensión de la física, te recomendamos familiarizarte con esta forma de expresión.

Cuál es el papel de las magnitudes físicas en las ecuaciones y leyes de la física

Las magnitudes físicas desempeñan un papel fundamental en las ecuaciones y leyes de la física, ya que son utilizadas para cuantificar y describir diferentes aspectos del mundo natural. Estas magnitudes son de suma importancia, ya que permiten realizar mediciones precisas, establecer relaciones matemáticas entre variables y formular leyes que rigen el comportamiento de los fenómenos físicos.

En la física, una magnitud física se define como una propiedad o característica mensurable que puede ser expresada numéricamente. Las magnitudes físicas se clasifican en dos categorías principales: magnitudes escalares y magnitudes vectoriales. Tanto las magnitudes escalares como las vectoriales son utilizadas en diferentes ramas de la física, aunque tienen características y representaciones distintas.

Magnitudes escalares

Las magnitudes escalares son aquellas que pueden ser completamente descritas por un número y una unidad. Esto significa que un número único es suficiente para determinar completamente la magnitud escalar, sin necesidad de especificar una dirección o sentido. Algunos ejemplos de magnitudes escalares son la masa, la temperatura, la longitud, el tiempo, la energía y la velocidad escalar.

Para representar las magnitudes escalares en una ecuación o ley física, generalmente se utiliza una letra en cursiva, como "m" para la masa y "T" para la temperatura. Además, es común utilizar unidades de medida, como kilogramos (kg) para la masa y grados Celsius (°C) para la temperatura, para indicar la escala o cantidad específica de la magnitud escalar.

Magnitudes vectoriales

A diferencia de las magnitudes escalares, las magnitudes vectoriales son aquellas que tienen tanto magnitud como dirección. Esto significa que una magnitud vectorial no solo tiene un valor numérico, sino también una orientación espacial. Algunos ejemplos comunes de magnitudes vectoriales son la velocidad, la aceleración, la fuerza, el momento lineal y el campo eléctrico.

Para representar las magnitudes vectoriales en una ecuación o ley física, es común utilizar una letra en negrita o con una flecha encima, como "v" para la velocidad y "F" para la fuerza. Además del valor numérico y la unidad, es necesario especificar también la dirección y sentido de la magnitud vectorial. Esto se puede hacer utilizando coordenadas cartesianas, ángulos o incluso diagramas vectoriales.

Importancia de distinguir entre magnitudes escalares y vectoriales

La distinción entre magnitudes escalares y magnitudes vectoriales es esencial en la física, ya que afecta directamente cómo se manejan y operan las diferentes cantidades físicas en ecuaciones y leyes. Por ejemplo, en una suma de magnitudes vectoriales, no solo se deben sumar los valores numéricos, sino también tener en cuenta la dirección y sentido de cada magnitud vectorial para obtener el vector resultado.

Además, las magnitudes vectoriales están sujetas a operaciones matemáticas específicas, como el producto escalar y el producto vectorial, que permiten obtener nuevas magnitudes o relaciones entre magnitudes vectoriales. Estas operaciones son fundamentales en muchas áreas de la física, como la dinámica, la cinemática, la electromagnetismo y la mecánica cuántica.

Las magnitudes físicas son piezas fundamentales en las ecuaciones y leyes de la física. Tanto las magnitudes escalares como las vectoriales desempeñan un papel esencial en la descripción y cuantificación de los fenómenos físicos. Es importante comprender la diferencia entre estas dos categorías de magnitudes, así como sus representaciones y operaciones matemáticas asociadas, para mejorar nuestra comprensión de la física y su aplicación en el mundo real.

Preguntas frecuentes (FAQ)

1. ¿Qué es una magnitud física?

Una magnitud física es una propiedad o característica de un objeto que puede medirse y expresarse mediante un número y una unidad.

2. ¿Cuál es la diferencia entre una magnitud escalar y una magnitud vectorial?

Una magnitud escalar solo tiene en cuenta su valor numérico, mientras que una magnitud vectorial incluye tanto su valor numérico como su dirección y sentido.

3. ¿Cómo se clasifican las magnitudes físicas?

Las magnitudes físicas se clasifican en fundamentales y derivadas. Las magnitudes fundamentales son aquellas que no pueden ser definidas en función de otras, como la masa, longitud y tiempo. Las magnitudes derivadas son aquellas que se obtienen a partir de las fundamentales, como la velocidad, aceleración y fuerza.

4. ¿Cuál es la diferencia entre una magnitud fundamental y una unidad fundamental?

Una magnitud fundamental es una propiedad física, mientras que una unidad fundamental es una convención establecida para medir esa magnitud.

5. ¿Por qué es importante conocer las magnitudes físicas?

Es importante conocer las magnitudes físicas porque nos permiten describir y comprender el mundo que nos rodea, y son fundamentales para el estudio y desarrollo de la física y otras ciencias.