¡Descubre cuánto mide la diagonal de un cuadrado y sorpréndete con este dato asombroso!

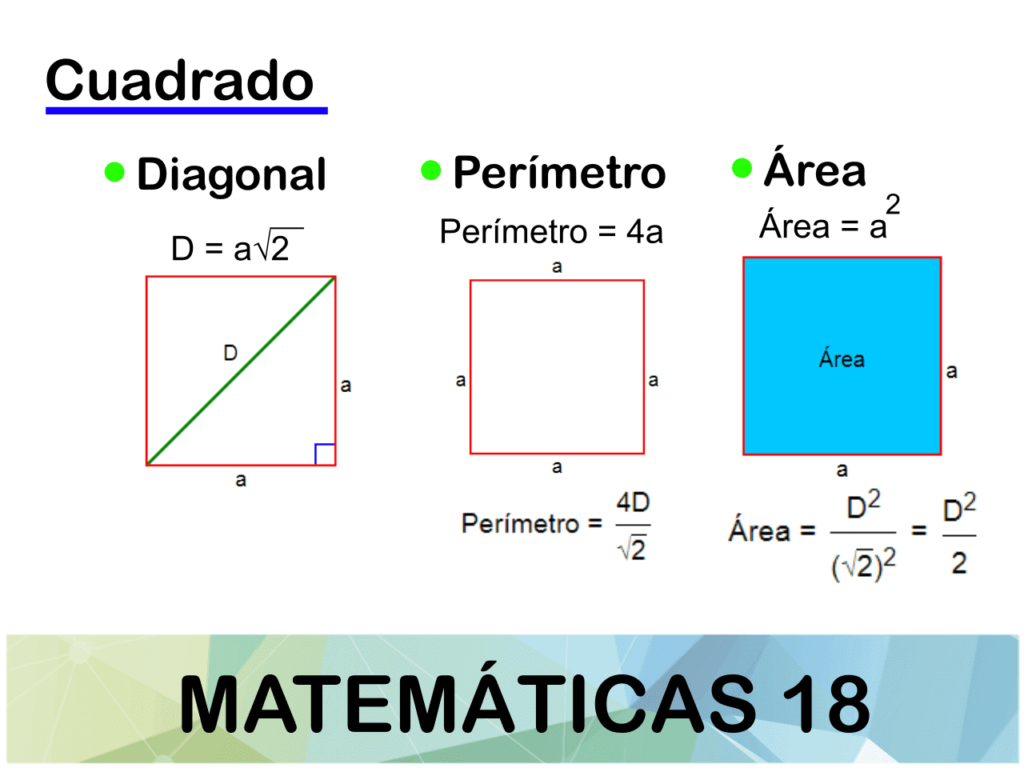
El cuadrado es una de las formas geométricas más conocidas y estudiadas. Su simplicidad y simetría han generado interés en muchas personas a lo largo de la historia. Una de las propiedades más fascinantes del cuadrado es su diagonal, y en este artículo exploraremos el concepto de la diagonal de un cuadrado y descubriremos cuánto mide exactamente.

Analizaremos detenidamente el concepto de diagonal en un cuadrado y cómo se relaciona con los lados de esta forma geométrica. También veremos cómo calcular la longitud de la diagonal y brindaremos algunos ejemplos prácticos para ilustrar mejor el tema. Si te interesa la geometría o simplemente quieres saber más sobre el cuadrado y sus características, ¡sigue leyendo para descubrir este dato asombroso!

Qué es la diagonal de un cuadrado y cómo se calcula

La diagonal de un cuadrado es una línea imaginaria que conecta dos vértices opuestos del mismo. Es decir, atraviesa el interior del cuadrado desde una esquina hasta la esquina opuesta. Esta línea es única para cada cuadrado y tiene propiedades matemáticas fascinantes.

Para calcular la longitud de la diagonal de un cuadrado, necesitamos utilizar el teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.

En el caso del cuadrado, tenemos un triángulo rectángulo isósceles, lo que significa que sus dos catetos (los lados iguales) también son las diagonales del cuadrado. Llamaremos "d" a la longitud de la diagonal del cuadrado y "l" al lado del cuadrado.

d = l * √2

Por lo tanto, si conocemos la longitud de uno de los lados del cuadrado, podemos calcular la longitud de su diagonal multiplicando ese lado por la raíz cuadrada de 2.

Cuánto mide la diagonal de un cuadrado con lados de longitud 5 cm

Si tenemos un cuadrado con lados de longitud 5 cm, podemos aplicar la fórmula anterior para obtener la medida de su diagonal.

d = 5 cm * √2 ≈ 7.07 cm

Por lo tanto, la diagonal de un cuadrado con lados de longitud 5 cm es aproximadamente 7.07 cm.

Por qué la diagonal de un cuadrado es mayor que sus lados

La razón por la cual la diagonal de un cuadrado es mayor que sus lados tiene que ver con el teorema de Pitágoras que mencionamos anteriormente. Como la diagonal del cuadrado forma un triángulo rectángulo con los lados del mismo, la longitud de la diagonal es la hipotenusa de ese triángulo.

El teorema de Pitágoras establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. En el caso del cuadrado, los dos catetos son iguales a la longitud de sus lados. Por lo tanto, al elevar al cuadrado la longitud de los lados y sumarlos, obtenemos un valor que es menor al cuadrado de la diagonal.

La diagonal de un cuadrado siempre será mayor que sus lados debido a las propiedades geométricas y matemáticas de los triángulos rectángulos.

Cuál es la fórmula para calcular la longitud de la diagonal de un cuadrado

Si estás buscando saber cuánto mide la diagonal de un cuadrado, estás en el lugar correcto. La fórmula para calcular la longitud de la diagonal de un cuadrado es una cuestión básica pero crucial en geometría. La diagonal de un cuadrado se refiere a la línea recta que une dos vértices opuestos del cuadrado.

Para entender mejor la fórmula, primero recordemos algunas propiedades del cuadrado. Un cuadrado es un polígono de cuatro lados iguales y cuatro ángulos rectos. Es un caso especial de un rectángulo, ya que todos sus lados tienen la misma longitud. Por lo tanto, si conoces la medida de un lado de un cuadrado, puedes usar esa información para calcular la longitud de su diagonal.

Ahora, para averiguar exactamente cuánto mide la diagonal de un cuadrado, necesitamos recurrir al teorema de Pitágoras. Según este famoso teorema, en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.

Aplicando este teorema al cuadrado, podemos considerar cada uno de los lados como un cateto, y la diagonal como la hipotenusa del triángulo rectángulo. Llamemos a la medida del lado del cuadrado "l", y la medida de la diagonal "d". Podemos escribir la ecuación:

d^2 = l^2 + l^2

Simplificando la ecuación, llegamos a:

d^2 = 2l^2

Para despejar la longitud de la diagonal, debemos encontrar la raíz cuadrada de ambos lados de la ecuación:

d = √(2l^2)

Por lo tanto, la fórmula para determinar la longitud de la diagonal de un cuadrado es:

d = √(2l^2)

Ahora que conoces la fórmula, puedes calcular la longitud de la diagonal de cualquier cuadrado dado su lado. Esto te puede resultar muy útil en problemas de geometría o al diseñar y construir estructuras cuadradas. Además, este dato asombroso sobre la diagonal del cuadrado puede sorprenderte y hacer que aprecies aún más las maravillas de las matemáticas y la geometría. ¡No pierdas la oportunidad de explorar el mundo fascinante de la geometría!

Cuánto mide la diagonal de un cuadrado de lado 4 unidades

Los cuadrados son figuras geométricas muy conocidas y estudiadas en matemáticas. Su estructura simétrica y sus ángulos rectos los hacen especialmente interesantes para realizar cálculos. Uno de los datos más curiosos que se puede obtener de un cuadrado es la medida de su diagonal.

La diagonal de un cuadrado se define como el segmento que une dos vértices no adyacentes del cuadrado. Es decir, es la línea recta que atraviesa el interior del cuadrado desde una esquina hasta la esquina opuesta, pasando por el centro. Este dato nos permite calcular la longitud de la diagonal utilizando el teorema de Pitágoras.

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. En el caso del cuadrado, la diagonal forma un triángulo rectángulo con los lados del cuadro como catetos y la diagonal como hipotenusa.

Si conocemos la medida de los lados del cuadrado, podemos utilizar el teorema de Pitágoras para hallar la longitud de la diagonal. Por ejemplo, si consideramos un cuadrado de lado 4 unidades, podemos seguir estos pasos:

1. Elevamos al cuadrado la medida de uno de los lados: 4^2 = 16.
2. Elevamos al cuadrado la medida del otro lado: 4^2 = 16.
3. Sumamos ambos resultados: 16 + 16 = 32.
4. Calculamos la raíz cuadrada de la suma obtenida: √32 ≈ 5.66 unidades.

Por lo tanto, la medida de la diagonal de un cuadrado de lado 4 unidades es aproximadamente 5.66 unidades. Este resultado nos muestra que la diagonal siempre será mayor que los lados del cuadrado, ya que se trata del segmento más largo que une dos vértices no adyacentes.

Es importante destacar que este cálculo aplica para cuadrados perfectos, es decir, cuadrados cuyos lados tienen una longitud igual. En el caso de cuadrados rectángulos o cuadrados cuyos lados tienen distintas medidas, el cálculo de la diagonal requiere de fórmulas adicionales.

Conocer la medida de la diagonal de un cuadrado nos permite comprender mejor su estructura y realizar diversos cálculos geométricos. Además, es un dato interesante que demuestra cómo las matemáticas nos brindan información acerca de las propiedades de las figuras geométricas.

Cuánto mide la diagonal de un cuadrado de lado 10 centímetros

Si quieres descubrir cuánto mide la diagonal de un cuadrado de lado 10 centímetros, estás en el lugar indicado. Este dato asombroso te dejará sorprendido y te ayudará a comprender mejor las propiedades geométricas de los cuadrados.

Primero, recordemos que un cuadrado es una figura geométrica con cuatro lados iguales y cuatro ángulos rectos. Esto significa que todos los lados de un cuadrado tienen la misma longitud. En este caso, estamos hablando de un cuadrado con un lado de 10 centímetros.

Para calcular la longitud de la diagonal de un cuadrado, podemos utilizar el teorema de Pitágoras. De acuerdo con este teorema, en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

En nuestro caso, consideraremos uno de los lados del cuadrado como uno de los catetos y la diagonal como la hipotenusa. Si llamamos "d" a la longitud de la diagonal, podemos aplicar el teorema de Pitágoras de la siguiente manera:

d^2 = L^2 + L^2

Donde "L" representa la longitud de uno de los lados del cuadrado. Para nuestro cuadrado de lado 10 centímetros, sustituimos "L" por 10 en la ecuación anterior:

d^2 = 10^2 + 10^2

Resolviendo esta ecuación, tenemos:

d^2 = 100 + 100
d^2 = 200

Entonces, la ecuación final para calcular la diagonal del cuadrado es:

d = sqrt(200)

Utilizando una calculadora, podemos encontrar que la raíz cuadrada de 200 es aproximadamente 14.14. Esto significa que la diagonal de un cuadrado de lado 10 centímetros mide aproximadamente 14.14 centímetros.

Es importante destacar que esta fórmula puede aplicarse a cualquier cuadrado, no solo al que hemos trabajado en este ejemplo. Si conoces la longitud de uno de los lados de un cuadrado, puedes utilizar el teorema de Pitágoras para calcular su diagonal sin importar cuánto mida.

La diagonal de un cuadrado de lado 10 centímetros es de aproximadamente 14.14 centímetros. Este dato asombroso demuestra las propiedades geométricas de los cuadrados y nos permite ampliar nuestro conocimiento sobre figuras geométricas.

Cuál es la relación entre la longitud de la diagonal y el lado de un cuadrado

La relación entre la longitud de la diagonal y el lado de un cuadrado es un tema fascinante que ha intrigado a matemáticos y entusiastas durante siglos. El descubrimiento de esta relación permite comprender mejor las propiedades geométricas de los cuadrados y revela un dato asombroso sobre su estructura.

Para entender esta relación, primero debemos recordar que un cuadrado es una figura geométrica con cuatro lados iguales y cuatro ángulos rectos. Cada uno de sus lados tiene la misma longitud, lo cual lo distingue de otras formas poligonales. La diagonal, por otro lado, es una línea que conecta dos vértices no adyacentes del cuadrado, atravesando su interior.

El dato asombroso es que la longitud de la diagonal de un cuadrado está relacionada directamente con la longitud de sus lados mediante una fórmula sencilla y elegante. Si llamamos "l" a la longitud de cada lado del cuadrado y "d" a la longitud de la diagonal, podemos establecer la siguiente relación:

d = l * √2

Esta fórmula nos indica que la longitud de la diagonal es igual a la longitud del lado multiplicada por la raíz cuadrada de 2. Con esta ecuación, podemos determinar fácilmente cuánto mide la diagonal de cualquier cuadrado conocida la longitud de su lado, o viceversa.

Aplicaciones prácticas de la relación entre la diagonal y el lado de un cuadrado

La comprensión de esta relación tiene diversas aplicaciones prácticas en diferentes campos, como la arquitectura, la ingeniería y el diseño de objetos. Por ejemplo, al diseñar una casa cuadrada, conocer la longitud de la diagonal permite determinar si ciertos muebles o estructuras podrán pasar a través de las puertas y pasillos con facilidad.

En el ámbito de la tecnología, esta relación también es relevante. Las pantallas cuadradas, ya sean de televisores, monitores o dispositivos móviles, también están sujetas a la misma relación entre la diagonal y el lado. Por lo tanto, conocer la longitud de la diagonal nos brinda información sobre el tamaño real de la pantalla y su utilidad en términos de visualización de contenido.

Otra aplicación interesante se encuentra en el ámbito de la carpintería. Al construir estantes cuadrados, conocer la longitud de la diagonal nos ayuda a calcular de manera precisa el espacio disponible para almacenar objetos, evitando así sorpresas desagradables cuando los objetos no caben debido a una falta de consideración de la diagonal.

• La relación entre la longitud de la diagonal y el lado de un cuadrado es una propiedad matemática fascinante que revela datos asombrosos sobre la estructura de esta figura geométrica.
• La fórmula sencilla d = l * √2 nos permite relacionar estas dos medidas de manera directa y precisa.
• Esta relación tiene aplicaciones prácticas en campos como la arquitectura, la ingeniería y el diseño.
• Saber cómo utilizar esta relación puede ayudarnos a tomar decisiones más informadas al diseñar o construir objetos cuadrados.

El conocimiento de la relación entre la longitud de la diagonal y el lado de un cuadrado no solo es útil desde el punto de vista matemático, sino que también tiene aplicaciones prácticas en diversos campos. Esta propiedad geométrica nos invita a reflexionar sobre las estructuras y formas presentes en nuestro entorno cotidiano, desvelando datos asombrosos que nos permiten comprender mejor el mundo que nos rodea.

Cuánto mide la diagonal de un cuadrado de área 25 metros cuadrados

La diagonal de un cuadrado es una de esas medidas que nos pueden sorprender con su resultado. A simple vista, uno podría pensar que la distancia entre dos vértices opuestos de un cuadrado es igual a su lado, pero eso no es del todo cierto. En realidad, la *diagonal* de un cuadrado puede ser calculada gracias al famoso teorema de Pitágoras.

Para entender cómo funciona este cálculo, primero debemos recordar que un cuadrado tiene todos sus lados iguales. Por lo tanto, si sabemos el área del cuadrado y queremos conocer la longitud de su diagonal, podemos utilizar la fórmula del área para despejar la medida de un lado.

Área = *lado x lado*

Si el área del cuadrado es de *25 metros cuadrados*, entonces tenemos:

25 = *lado x lado*

Ahora, mediante una operación matemática sencilla, podemos despejar la medida de un lado:

lado = *√25*

Resolviendo esta raíz cuadrada, obtenemos que el lado del cuadrado es igual a *5 metros*.

Una vez que conocemos la medida de un lado del cuadrado, podemos aplicar el teorema de Pitágoras para calcular la longitud de la *diagonal*. Según este teorema, en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los otros dos lados.

En el caso de un cuadrado, la diagonal es justamente la hipotenusa de un triángulo rectángulo formado por dos lados del cuadrado. Entonces, tenemos:

*hipotenusa^2 = lado^2 + lado^2*

Sustituyendo el valor del lado que obtuvimos previamente, podemos calcular la longitud de la *diagonal*:

*hipotenusa^2 = 5^2 + 5^2*
*hipotenusa^2 = 25 + 25*
*hipotenusa^2 = 50*

Realizando la raíz cuadrada de ambos lados de la ecuación, encontramos que:

*hipotenusa = √50*

Resolviendo esta última raíz cuadrada, obtenemos aproximadamente que la longitud de la *diagonal* del cuadrado es igual a *7.07 metros*.

¡Es impresionante cómo una figura tan simple como un cuadrado puede esconder datos asombrosos como este! La longitud de su *diagonal* no es simplemente igual a la medida de su lado, sino que requiere de un cálculo y la aplicación del teorema de Pitágoras. ¡No olvides lo fascinante y sorprendente que puede ser las matemáticas!

Por qué la diagonal de un cuadrado es mayor que su lado

¡La diagonal de un cuadrado es una característica fascinante y sorprendente! A simple vista, puede parecer que la diagonal de un cuadrado debería ser igual a su lado, ya que todas sus caras son perpendiculares entre sí y tienen la misma longitud. Sin embargo, esto no es así. La realidad es que la diagonal de un cuadrado siempre será mayor que su lado.

Para entender por qué sucede esto, es necesario desglosar un poco las características geométricas de un cuadrado. Como sabemos, un cuadrado es un polígono de cuatro lados iguales y cuatro ángulos rectos. Esto significa que cada uno de sus lados tiene exactamente la misma longitud, lo cual es fundamental para su definición y propiedades.

Una manera sencilla de visualizar la magnitud de la diagonal es imaginando un triángulo rectángulo formado por dos lados del cuadrado y la propia diagonal. Al trazar esta línea imaginaria, podemos notar que se crea un ángulo perfecto de 90 grados entre la diagonal y cada uno de los lados del cuadrado. Este ángulo recto es el que hace posible la relación especial entre la longitud del lado y la diagonal.

Si tomamos la longitud de uno de los lados del cuadrado como "a" y aplicamos el teorema de Pitágoras al triángulo rectángulo, obtendremos la expresión matemática para calcular la longitud de la diagonal: D² = a² + a². Simplificando, nos quedaría D² = 2a².

¿Qué significa esto? Que para encontrar la longitud de la diagonal, debemos tomar la raíz cuadrada de 2 multiplicada por la longitud del lado del cuadrado. Es decir, D = √2 * a. Como el número √2 es aproximadamente 1.41, podemos concluir que la longitud de la diagonal de un cuadrado siempre será aproximadamente 1.41 veces mayor que la longitud de uno de sus lados.

Este resultado lleva a una interesante reflexión sobre las proporciones y la geometría. A simple vista, podríamos pensar que la diagonal debería ser igual al lado debido a la simetría que presenta el cuadrado. Sin embargo, la diagonal termina siendo mayor debido a la relación especial entre los ángulos rectos y la longitud de cada lado. ¡La sorpresa de descubrir este dato asombroso nos muestra lo fascinante que puede ser el mundo de las matemáticas!

Cómo se puede usar la diagonal de un cuadrado en problemas de geometría

La geometría es una rama de las matemáticas que estudia las propiedades y las relaciones de las figuras en el espacio. Una de las figuras más básicas es el cuadrado, que tiene cuatro lados iguales y cuatro ángulos rectos.

¿Qué es la diagonal de un cuadrado?

La diagonal de un cuadrado es una línea recta que une dos vértices no adyacentes del cuadrado. Es importante destacar que la longitud de la diagonal es mayor que los lados del cuadrado. La relación entre la diagonal y los lados puede calcularse utilizando el Teorema de Pitágoras.

Cálculo de la diagonal de un cuadrado

Para calcular la longitud de la diagonal de un cuadrado, podemos utilizar la fórmula:

d = l × √2

donde d representa la longitud de la diagonal y l representa la longitud de los lados del cuadrado.

Por ejemplo, si tenemos un cuadrado con lados de longitud 10 cm, podemos calcular la diagonal utilizando la fórmula anterior:

d = 10 × √2 ≈ 14.142 cm

Por lo tanto, la longitud aproximada de la diagonal sería de 14.142 cm.

Aplicaciones de la diagonal de un cuadrado

La diagonal de un cuadrado tiene diversas aplicaciones en problemas de geometría y matemáticas en general. Algunas de estas aplicaciones incluyen:

• Cálculo del perímetro de un rombo: Un rombo es un cuadrilátero con lados iguales, pero sus ángulos no necesariamente son de 90 grados. Si conocemos la longitud de la diagonal y sabemos que los lados del rombo son congruentes, podemos calcular el perímetro utilizando la fórmula P = d × 2.
• Determinación de la distancia entre dos puntos: Si conocemos las coordenadas de dos puntos en un plano cartesiano y estos puntos forman una diagonal del cuadrado, podemos utilizar la distancia entre dos puntos para determinar la longitud de la diagonal.
• Cálculo del área de un rectángulo: Un rectángulo es un caso especial de un cuadrado donde los ángulos no necesariamente son de 90 grados. Si sabemos que la diagonal es igual a la hipotenusa de un triángulo rectángulo formado por los lados del rectángulo, podemos utilizar el Teorema de Pitágoras para calcular la longitud de los lados y, posteriormente, calcular el área con la fórmula A = l1 × l2.

Como podemos ver, la diagonal de un cuadrado no solo es un dato asombroso, sino que también tiene múltiples aplicaciones en problemas de geometría y matemáticas. Su cálculo puede ayudarnos a resolver diferentes tipos de ejercicios y nos permite comprender mejor las propiedades de esta figura geométrica básica.

Cuál es el concepto de "teorema de Pitágoras" y cuál es su relación con la diagonal de un cuadrado

El teorema de Pitágoras es uno de los conceptos fundamentales de la geometría euclidiana y establece una relación entre las longitudes de los lados de un triángulo rectángulo. Fue descubierto por el matemático griego Pitágoras en el siglo VI a.C. y sigue siendo ampliamente utilizado en diversas ramas de las matemáticas y ciencias aplicadas.

Este teorema establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos. Es decir, si denotamos la hipotenusa como c y los catetos como a y b, entonces podemos expresarlo mediante la fórmula:

c^2 = a^2 + b^2

La relación entre el teorema de Pitágoras y la diagonal de un cuadrado radica en que un cuadrado es un tipo especial de triángulo rectángulo. En un cuadrado, los cuatro ángulos son rectos y los cuatro lados tienen la misma longitud. Por lo tanto, podemos dividir un cuadrado en dos triángulos rectángulos congruentes, donde cada lado del cuadrado se convierte en un cateto.

Si llamamos a la longitud de un lado del cuadrado como a, entonces utilizando el teorema de Pitágoras, podemos calcular la longitud de la hipotenusa de uno de los triángulos rectángulos. Aplicando la fórmula, tenemos:

hipotenusa^2 = a^2 + a^2

Simplificando la expresión, obtenemos:

hipotenusa^2 = 2a^2

Finalmente, al calcular la raíz cuadrada de ambos lados de la ecuación, encontramos que la longitud de la hipotenusa -que en este caso es la diagonal del cuadrado- está dada por:

diagonal = √(2a^2)

Así que el teorema de Pitágoras nos permite determinar la longitud de la diagonal de un cuadrado conocida la longitud de uno de sus lados. Esta relación matemática tan sorprendente nos revela que la diagonal de un cuadrado es aproximadamente 1.414 veces más larga que uno de sus lados.

Cuál es la importancia de saber la medida de la diagonal de un cuadrado en el mundo real

La medida de la diagonal de un cuadrado puede ser un dato aparentemente trivial, pero en realidad es de gran importancia en el mundo real. Conocer esta medida nos permite desempeñar diversas actividades y cálculos necesarios en diferentes áreas, desde la construcción hasta la geometría y los diseños gráficos.

En el campo de la construcción, saber la medida de la diagonal de un cuadrado es esencial para asegurar la precisión y estabilidad de las estructuras. Al calcular la diagonal, se pueden determinar las dimensiones correctas de los elementos que componen dicha estructura, evitando problemas futuros y garantizando la seguridad de quienes la utilizarán.

Además, la diagonal de un cuadrado también juega un papel clave en la geometría. A través de ella, se pueden realizar diversos cálculos matemáticos y establecer relaciones entre las diferentes partes de una figura. Por ejemplo, al conocer la medida de la diagonal de un cuadrado, podemos calcular fácilmente la longitud de sus lados mediante el teorema de Pitágoras.

Aplicaciones prácticas de la medida de la diagonal de un cuadrado

Las aplicaciones prácticas de conocer la medida de la diagonal de un cuadrado son variadas y se encuentran presentes en numerosos aspectos de nuestra vida cotidiana.

• Diseño de espacios: En la arquitectura y el diseño de interiores, saber la medida de la diagonal de un cuadrado es fundamental para distribuir de manera eficiente el mobiliario y los objetos decorativos en un espacio determinado. Esto garantiza que no se generarán obstrucciones ni se desperdiciará espacio, logrando una mejor funcionalidad y estética en el ambiente.
• Corte de materiales: En trabajos relacionados con la carpintería, la medida de la diagonal de un cuadrado es esencial para realizar cortes precisos en tablas, paneles u otros materiales. Conociendo esta medida, se pueden calcular los ángulos necesarios y lograr uniones perfectas entre las distintas piezas, evitando espacios o desajustes indeseados.
• Diseño gráfico: En el ámbito del diseño gráfico, especialmente en la creación de logotipos o elementos visuales con formas cuadradas, conocer la medida de la diagonal de un cuadrado es fundamental para asegurar la proporción correcta y evitar distorsiones visuales. Esto es especialmente importante al trabajar con programas de edición de imágenes o diseño vectorial.

Como podemos ver, la medida de la diagonal de un cuadrado tiene múltiples aplicaciones en diferentes áreas de nuestra vida. Su importancia radica en que nos proporciona datos precisos que nos permiten realizar cálculos y tomar decisiones acertadas en diversos contextos. Por lo tanto, conocer y comprender este dato asombroso nos brinda una ventaja invaluable en nuestras actividades diarias.

Preguntas frecuentes (FAQ)

1. ¿Cuál es la fórmula para calcular la diagonal de un cuadrado?

La fórmula para calcular la diagonal de un cuadrado es d = l * √2, donde d es la diagonal y l es el lado del cuadrado.

2. ¿Qué relación hay entre la diagonal y el lado de un cuadrado?

La diagonal de un cuadrado es aproximadamente 1.414 veces más larga que su lado. Es decir, si el lado del cuadrado mide 1 unidad, la diagonal será aproximadamente 1.414 unidades.

3. ¿Por qué la diagonal de un cuadrado es mayor que su lado?

La diagonal de un cuadrado es mayor que su lado debido al teorema de Pitágoras. Al trazar una diagonal en un cuadrado, se forma un triángulo rectángulo isósceles, donde la hipotenusa (diagonal) es más larga que los catetos (lados).

4. ¿Qué utilidad tiene conocer la medida de la diagonal de un cuadrado?

Conocer la medida de la diagonal de un cuadrado es útil para determinar distancias diagonales en superficies cuadradas, como por ejemplo el tamaño de una pantalla, el recorrido de una ruta en un mapa o el tamaño de una habitación.

5. ¿La diagonal de un cuadrado siempre es un número irracional?

Sí, la diagonal de un cuadrado siempre es un número irracional. Esto significa que no se puede expresar como una fracción o un número decimal exacto, sino que tiene infinitas cifras decimales no repetitivas.