Descubre cuántos ejes de simetría tiene un trapecio y mejora tus habilidades matemáticas

La simetría es un concepto fundamental en matemáticas que se refiere a la igualdad de un objeto o figura respecto a una línea o punto. En el caso de los trapecios, que son cuadriláteros con al menos dos lados paralelos, también es posible encontrar ejes de simetría. Los ejes de simetría son líneas rectas que dividen una figura en dos partes iguales y cuyo reflejo coincidirá con la original. Identificar los ejes de simetría de un trapecio nos permite comprender mejor su estructura y explorar las propiedades de esta figura geométrica.

Te explicaremos cómo determinar cuántos ejes de simetría tiene un trapecio y cómo mejorar tus habilidades matemáticas en el proceso. Analizaremos diferentes casos en función de las características de los trapecios y proporcionaremos ejemplos prácticos para que puedas aplicar estos conceptos en tu aprendizaje. ¡No te lo pierdas!

Qué es un trapecio y cuáles son sus características principales

Un trapecio es un polígono de cuatro lados que se caracteriza por tener dos lados paralelos. Estos lados paralelos son conocidos como las bases del trapecio. Además, tiene dos lados no paralelos llamados las ramas o patas del trapecio. Es importante destacar que las bases pueden ser de diferente longitud, lo que hace al trapecio un polígono asimétrico.

El trapecio también se distingue por tener dos ángulos agudos y dos ángulos obtusos. Los ángulos agudos están ubicados entre las bases y las ramas, mientras que los ángulos obtusos están en la parte exterior de las bases.

Dentro de las características principales de un trapecio se encuentra su altura. La altura de un trapecio es la distancia perpendicular entre sus bases. Se puede calcular utilizando el teorema de Pitágoras o mediante fórmulas específicas según los datos proporcionados.

Otra característica relevante es el área de un trapecio. El área se calcula multiplicando la longitud de la base mayor por la altura y dividiendo el resultado entre 2. La fórmula exacta depende de si el trapecio es isósceles (ambas bases tienen la misma longitud) o escaleno (las bases tienen diferente longitud).

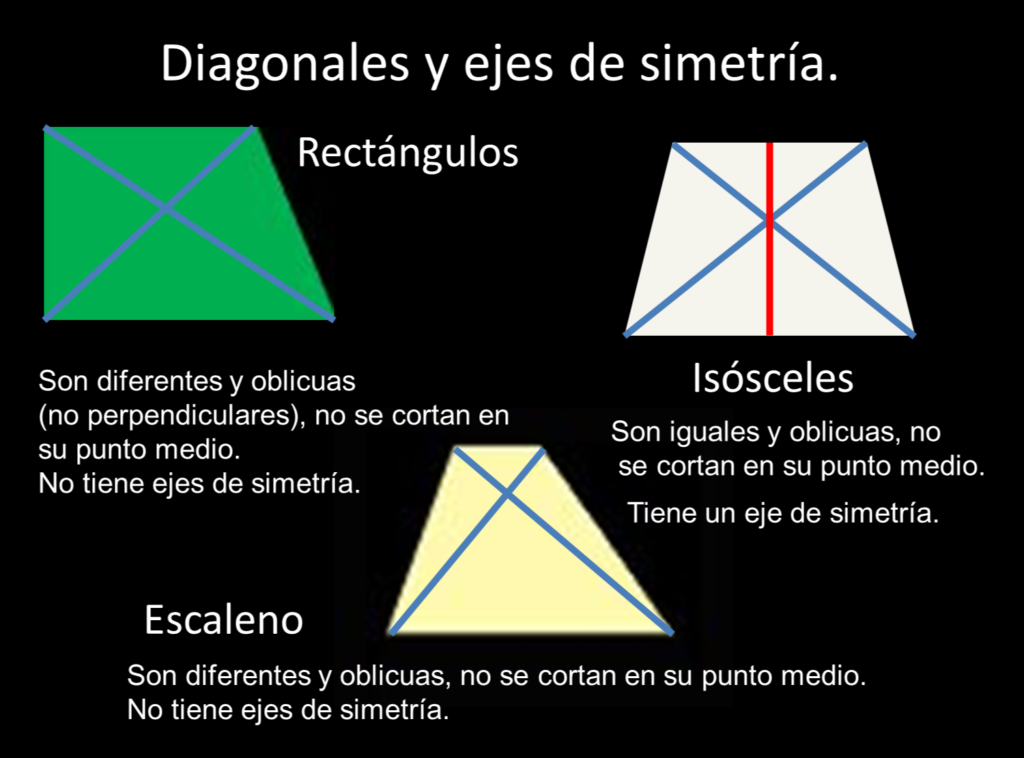
Cuántos ejes de simetría tiene un trapecio

Un eje de simetría de una figura plana es una línea imaginaria que divide a la figura en dos partes iguales, pero opuestas. En el caso del trapecio, la respuesta puede variar dependiendo de sus características específicas.

Si el trapecio es un trapezoide, es decir, tiene sus lados no paralelos de diferente longitud, entonces puede tener cero o un eje de simetría. Esto se debe a que no hay ninguna línea que divida la figura en partes iguales y opuestas.

Por otro lado, si el trapecio es un trapecio isósceles, es decir, tiene sus bases con la misma longitud, entonces siempre tiene uno o dos ejes de simetría. En un trapecio isósceles, la simetría se da al dibujar una línea imaginaria que pasa por el punto medio de las bases, dividiendo así la figura en dos partes idénticas y opuestas.

Un trapecio puede tener cero, uno o dos ejes de simetría, dependiendo de si es un trapezoide o un trapecio isósceles. Es importante recordar que los ejes de simetría proporcionan información sobre la estructura y propiedades geométricas de un trapecio, lo cual es útil para mejorar nuestras habilidades matemáticas y nuestro entendimiento del mundo que nos rodea.

Cuáles son los ejes de simetría en un trapecio

Un trapecio es un polígono de cuatro lados con dos lados paralelos y dos lados no paralelos. Una de las características más interesantes de los trapecios son sus ejes de simetría.

La simetría en geometría se refiere a la cualidad de una figura de ser idéntica en ambos lados de un eje o plano. En el caso de los trapecios, los ejes de simetría son líneas rectas que dividen la figura en dos partes iguales cuando se pliega a lo largo de ellas.

Para determinar cuántos ejes de simetría tiene un trapecio, debemos tener en cuenta su forma. Hay varios casos posibles:

Trapecio isósceles

En un trapecio isósceles, los lados no paralelos tienen la misma longitud. En este caso, el trapecio tiene un eje de simetría que pasa por el punto medio de los lados no paralelos y también es perpendicular a la base.

Este eje de simetría divide al trapecio en dos partes congruentes, lo que significa que ambas mitades son idénticas si se pliegan a lo largo de esta línea. Por lo tanto, el trapecio isósceles tiene un único eje de simetría.

Trapecio escaleno

En un trapecio escaleno, los lados no paralelos tienen longitudes diferentes. En este caso, no hay un eje de simetría definido ya que las partes del trapecio no son congruentes entre sí.

Por lo tanto, un trapecio escaleno no tiene ejes de simetría.

Trapecio rectángulo

Un trapecio rectángulo es aquel en el que uno de los ángulos internos es de 90 grados. En este caso, el trapecio tiene un único eje de simetría que pasa por el punto medio de la base y es perpendicular a ella.

Este eje de simetría divide al trapecio en dos partes congruentes, lo que significa que ambas mitades son idénticas si se pliegan a lo largo de esta línea. Por lo tanto, el trapecio rectángulo tiene un único eje de simetría.

El número de ejes de simetría en un trapecio depende de su forma. Un trapecio isósceles tiene un único eje de simetría, un trapecio escaleno no tiene ejes de simetría, y un trapecio rectángulo tiene un único eje de simetría también. Conocer estos conceptos te ayudará a mejorar tus habilidades matemáticas y comprender mejor las propiedades de los trapecios.

Cómo identificar los ejes de simetría en un trapecio

Un trapecio es un polígono de cuatro lados que posee dos lados paralelos y dos lados no paralelos. Si te preguntas cuántos ejes de simetría tiene un trapecio, debes comprender primero qué es un eje de simetría.

Un eje de simetría es una línea imaginaria que divide una figura en dos partes iguales y reflejadas. En otras palabras, si pudiéramos doblar la figura a lo largo de su eje de simetría, las dos partes resultantes serían superponibles.

En el caso de un trapecio, es importante tener en cuenta que los ejes de simetría solo se presentan en trapecios isósceles, es decir, aquellos que tienen ambos lados no paralelos de igual longitud. En un trapecio isósceles, hay un número específico de ejes de simetría dependiendo del tipo de trapecio:

Trapecio isósceles con ángulos bases iguales:

• Si ambos ángulos bases son iguales, el trapecio tiene un único eje de simetría. Este eje sería la línea perpendicular que divide el trapecio en dos partes reflectantes.

Trapecio isósceles con ángulos bases diferentes:

• Si los ángulos bases son diferentes pero ambos lados no paralelos son congruentes, entonces el trapecio tiene dos ejes de simetría. Los dos ejes serían las bisectrices de los ángulos bases, que dividen el trapecio en cuatro regiones congruentes.

Es importante recordar que un trapecio no isósceles, es decir, un trapecio con lados no paralelos de diferentes longitudes, no tiene ejes de simetría. Esto se debe a que no es posible dividir el trapecio en dos partes iguales mediante un eje de simetría debido a la falta de congruencia en los lados no paralelos.

Ahora que sabes cómo identificar los ejes de simetría en un trapecio, puedes mejorar tus habilidades matemáticas y aplicar este conocimiento en problemas y ejercicios relacionados con la geometría. Practicar la identificación de ejes de simetría en diferentes figuras te ayudará a fortalecer tu razonamiento espacial y visual, lo cual es fundamental en el estudio de las matemáticas.

¿Cuántos ejes de simetría puede tener un trapecio?

Un trapecio es un polígono que cuenta con cuatro lados, siendo dos de ellos paralelos y los otros dos no paralelos. Pero ¿cuántos ejes de simetría puede tener un trapecio?

Antes de responder a esa pregunta, es importante entender qué es un eje de simetría. Un eje de simetría es una línea imaginaria que divide al objeto en dos partes iguales, es decir, si doblamos el objeto a lo largo del eje de simetría, ambos lados serán exactamente iguales.

En el caso específico de un trapecio, podemos encontrar distintas posibilidades en cuanto a ejes de simetría. La cantidad exacta dependerá de las características del trapecio en cuestión.

Trapecios isósceles

Un trapecio isósceles es aquel en el que los lados no paralelos tienen la misma longitud. En este caso, existe un único eje de simetría, el cual es la línea que atraviesa el punto medio de los lados no paralelos.

Trapecios rectángulos

Por otro lado, tenemos los trapecios rectángulos, que son aquellos en los que uno de los ángulos internos mide 90 grados. Estos trapecios también cuentan con un único eje de simetría, que se encuentra perpendicular a sus bases y pasa por el punto medio de los lados no paralelos.

Trapecios escalenos

Los trapecios escalenos, que son aquellos en los que los lados no paralelos tienen longitudes diferentes, pueden tener hasta dos ejes de simetría. Estos ejes se ubican como líneas que atraviesan los puntos medios de los lados no paralelos y están equidistantes de las bases del trapecio.

La cantidad de ejes de simetría en un trapecio puede variar dependiendo de sus características geométricas. Los trapecios isósceles y rectángulos tienen un único eje de simetría, mientras que los trapecios escalenos pueden tener hasta dos ejes de simetría.

Comprender y reconocer los ejes de simetría en los trapecios es fundamental para mejorar nuestras habilidades matemáticas. Además, aprender sobre estas propiedades geométricas nos ayuda a comprender mejor las formas y su comportamiento en el espacio.

¿Cuál es la fórmula para calcular los ejes de simetría en un trapecio isósceles?

El concepto de simetría en la geometría juega un papel fundamental a la hora de analizar las propiedades de las figuras. En el caso específico de un trapecio, uno de los aspectos que se pueden analizar es la cantidad de ejes de simetría que posee. Estos ejes son líneas imaginarias que dividen a la figura en dos partes iguales al ser reflejados en ellos.

En el caso de un trapecio isósceles, es decir, aquel que tiene sus lados no paralelos de igual longitud, podemos determinar fácilmente cuántos ejes de simetría tiene mediante una fórmula sencilla. Para ello, debemos tener en cuenta algunas propiedades del trapecio y aplicar un poco de razonamiento matemático.

Propiedades de un trapecio isósceles

Un trapecio isósceles se caracteriza por tener dos lados no paralelos de igual longitud, lo cual implica que las bases son paralelas. Además, los ángulos opuestos entre los lados no paralelos también son congruentes.

Con estas propiedades en mente, podemos proceder a determinar la fórmula para calcular los ejes de simetría en un trapecio isósceles.

Fórmula para calcular los ejes de simetría

La fórmula para calcular los ejes de simetría en un trapecio isósceles viene dada por:

Ejes de simetría = n / 2

Donde n representa el número de lados del trapecio. En este caso, dado que un trapecio tiene 4 lados, la fórmula queda de la siguiente manera:

Ejes de simetría = 4 / 2 = 2

Por lo tanto, un trapecio isósceles tendrá 2 ejes de simetría.

Importancia de conocer los ejes de simetría en un trapecio

Saber cuántos ejes de simetría tiene un trapecio isósceles es importante para comprender mejor su estructura y propiedades geométricas. Los ejes de simetría nos permiten identificar los puntos de simetría y entender cómo se relacionan las diferentes partes de la figura.

Además, conocer los ejes de simetría puede ser útil al realizar construcciones geométricas o resolver problemas matemáticos que involucren trapecios. También es una habilidad importante en campos como la arquitectura, donde la simetría juega un papel fundamental en el diseño de estructuras.

Los ejes de simetría son una herramienta clave para analizar y comprender la estructura de un trapecio isósceles. Su cálculo sencillo nos permite obtener información valiosa sobre la figura y mejorar nuestras habilidades matemáticas.

¿Cómo se pueden mejorar las habilidades matemáticas al aprender sobre los ejes de simetría en un trapecio?

Los ejes de simetría son un tema importante en matemáticas que nos ayuda a comprender y analizar las propiedades geométricas de diferentes figuras. En este caso, nos enfocamos en el trapecio, una figura plana con cuatro lados, dos de los cuales son paralelos, llamados bases, y los otros dos lados son no paralelos, llamados lados laterales.

Un eje de simetría es una línea imaginaria que divide una figura en dos mitades iguales, como si fuera un espejo. En el caso del trapecio, ¿sabías que puede tener hasta un máximo de dos ejes de simetría?

Para encontrar los ejes de simetría en un trapecio, debemos observar la disposición de sus lados y ángulos. Si trazamos una línea desde uno de los vértices del trapecio hasta el punto medio de la base opuesta, obtendremos un eje de simetría. Este eje dividirá al trapecio en dos partes de igual área y forma.

Pero eso no es todo, porque en algunos casos es posible encontrar un segundo eje de simetría. Para ello, trazamos una línea que conecte los puntos medios de los lados laterales del trapecio. Esta línea también será un eje de simetría, dividiendo al trapecio en dos partes iguales.

Conocer los ejes de simetría en un trapecio no solo nos permite entender mejor su estructura geométrica, sino también mejorar nuestras habilidades matemáticas. Al estudiar y analizar la simetría en el trapecio, desarrollaremos habilidades de observación, razonamiento y visualización espacial.

Además, trabajar con los ejes de simetría en el trapecio nos ayudará a fortalecer nuestra comprensión de otros conceptos matemáticos relacionados, como la medición de ángulos y segmentos, las propiedades de las figuras planas y la geometría en general. También será útil cuando enfrentemos problemas o situaciones reales que requieran aplicar estos conocimientos.

Aprender sobre los ejes de simetría en un trapecio es una excelente forma de mejorar nuestras habilidades matemáticas. Nos permite comprender mejor la estructura y las propiedades de esta figura geométrica, desarrollando habilidades clave como la observación, el razonamiento y la visualización espacial. Así que no dudes en explorar y practicar este concepto matemático para llevar tus habilidades al siguiente nivel.

¿Cuáles son los beneficios de comprender los ejes de simetría en matemáticas?

Comprender los ejes de simetría en matemáticas puede proporcionar una serie de beneficios tanto en el ámbito académico como en la vida cotidiana. Los ejes de simetría son líneas imaginarias que dividen una figura en dos partes exactamente iguales y se utilizan para estudiar la simetría en geometría.

Uno de los beneficios más evidentes de comprender los ejes de simetría es poder identificarlos correctamente en figuras geométricas, como en el caso del trapecio. El trapecio es un polígono con cuatro lados, dos de los cuales son paralelos y los otros dos no lo son. Al comprender los ejes de simetría en un trapecio, podemos determinar cuántos ejes de simetría tiene y cómo afecta a su forma y propiedades.

Mejora tus habilidades matemáticas

Al estudiar y comprender los ejes de simetría en matemáticas, estaremos fortaleciendo nuestras habilidades matemáticas de diversas formas. Primero, nos ayudará a desarrollar nuestra capacidad de visualización espacial, ya que tendremos que imaginar las líneas de simetría y cómo afectan la figura. Esto puede ser especialmente útil en problemas de geometría donde necesitamos visualizar y manipular figuras en tres dimensiones.

Además, comprender los ejes de simetría puede mejorar nuestras habilidades de deducción y razonamiento lógico. Al analizar la simetría en una figura, tendremos que realizar inferencias y llegar a conclusiones sobre sus propiedades. Esto nos permite aplicar conceptos matemáticos, como la reflexión y la traslación, para resolver problemas más complejos.

Asimismo, comprender los ejes de simetría puede mejorar nuestra capacidad para identificar patrones y regularidades en las figuras geométricas. Al observar cómo se repiten las simetrías en diferentes partes de una figura, podemos establecer conexiones entre conceptos y desarrollar una comprensión más profunda de las propiedades y características de las formas.

Aplicaciones prácticas

Aunque estudiar los ejes de simetría puede parecer una habilidad abstracta, tiene aplicaciones prácticas en varios campos de estudio y profesiones. En arquitectura y diseño, comprender y utilizar adecuadamente la simetría puede ayudar a crear estructuras y diseños estéticamente agradables y equilibrados.

En el campo de la física, la simetría es un concepto fundamental en muchas teorías y modelos científicos. Comprender los ejes de simetría puede ser útil para comprender conceptos como los campos electromagnéticos, las leyes del movimiento y las estructuras moleculares.

Incluso en el mundo natural, la simetría es una característica común en muchas formas de vida y fenómenos naturales. Comprender los ejes de simetría puede ayudarnos a apreciar la belleza y la perfección de la geometría en la naturaleza, desde las formas de los cristales hasta los patrones de las alas de una mariposa.

Comprender los ejes de simetría en matemáticas va más allá de ser simplemente un concepto abstracto. Mejora nuestras habilidades matemáticas, desarrolla nuestras capacidades de visualización y razonamiento lógico, y tiene aplicaciones prácticas en diversos campos. Así que no subestimes el poder de comprender la simetría y cómo puede mejorar tus habilidades matemáticas y tu comprensión del mundo que te rodea.

Dónde se aplican los conocimientos sobre los ejes de simetría en el mundo real

Los conocimientos sobre los ejes de simetría no solo son útiles en el ámbito matemático, sino que también se aplican en diversas áreas del mundo real. La simetría es una propiedad que está presente en muchas cosas que nos rodean, desde objetos cotidianos hasta estructuras arquitectónicas impresionantes.

En el campo del diseño gráfico, por ejemplo, los ejes de simetría son fundamentales para lograr composiciones equilibradas y atractivas visualmente. Los diseñadores utilizan los principios de simetría para crear logotipos, ilustraciones y diseños digitales que transmiten armonía y orden.

También en la naturaleza podemos encontrar ejemplos de simetría. Muchas flores presentan una simetría radial, lo que significa que se pueden dividir en varias partes iguales alrededor de un eje central. Esto no solo las hace estéticamente agradables, sino que también facilita la polinización al atraer a los insectos polinizadores desde diferentes direcciones.

Incluso en el campo de la medicina, el conocimiento de los ejes de simetría es relevante. Los médicos y cirujanos a menudo utilizan la simetría corporal como referencia para diagnosticar enfermedades o planificar intervenciones quirúrgicas. Por ejemplo, la cara humana tiene una simetría bilateral que permite a los profesionales de la medicina identificar anomalías o lesiones.

Además, la simetría también tiene su lugar en la decoración de interiores. Los diseñadores de interiores utilizan patrones y elementos simétricos para crear espacios armónicos y equilibrados. El uso de espejos, muebles y accesorios con simetría puede hacer que una habitación se sienta más acogedora y organizada.

Como podemos ver, el conocimiento sobre los ejes de simetría trasciende las matemáticas y se aplica en diversas áreas de nuestras vidas. Ya sea en el arte, la naturaleza, la medicina o la decoración, comprender y reconocer la simetría nos permite apreciar la belleza y la armonía presentes en nuestro entorno.

Preguntas frecuentes (FAQ)

1. ¿Cuántos ejes de simetría tiene un trapecio?

Un trapecio puede tener hasta un máximo de 2 ejes de simetría.

2. ¿Cuáles son las características de un trapecio isósceles?

Un trapecio isósceles tiene dos lados paralelos y dos ángulos congruentes en su base.

3. ¿Qué diferencia hay entre un trapecio y un trapecio rectángulo?

Un trapecio rectángulo tiene uno de sus ángulos interiores rectos, mientras que en un trapecio común no necesariamente ocurre esto.

4. ¿Cuál es la fórmula para calcular el área de un trapecio?

El área de un trapecio se calcula multiplicando la suma de la longitud de sus bases por la altura, y dividiendo el resultado entre 2.

5. ¿Cómo puedo determinar si un trapecio es un trapecio equilátero?

Un trapecio equilátero es aquel en el que sus cuatro lados tienen la misma longitud.