Fórmula infalible: ¡Calcula el vértice de una parábola en segundos! Aprende ahora mismo

Las parábolas son una de las formas más comunes de ecuaciones cuadráticas. Son curvas simétricas que se abren hacia arriba o hacia abajo y tienen un punto especial llamado vértice. El vértice de una parábola tiene importantes propiedades y es útil para resolver problemas matemáticos y graficar la función.

Aprenderás cómo encontrar el vértice de una parábola usando la fórmula infalible. Te enseñaremos paso a paso cómo aplicarla y conocerás todos los detalles para realizar el cálculo en segundos. Además, daremos algunos ejemplos prácticos para que puedas practicar y dominar el concepto. No importa si eres estudiante o simplemente quieres refrescar tus conocimientos de geometría, ¡este artículo te será de gran ayuda!

Qué es el vértice de una parábola y por qué es importante calcularlo

El vértice de una parábola es un punto crucial en su gráfica que nos proporciona información importante sobre su forma y posición. Es el punto más alto o más bajo de la parábola, dependiendo de si esta se abre hacia arriba o hacia abajo. Calcular el vértice de una parábola nos permite determinar su concavidad, así como el desplazamiento horizontal y vertical de la función cuadrática.

La importancia de calcular el vértice radica en que nos permite obtener información valiosa sobre diferentes situaciones de la vida real. En física, por ejemplo, conocer el vértice de una parábola puede ayudarnos a determinar la altura máxima alcanzada por un objeto lanzado al aire o el tiempo en el que esto ocurre. En economía, calcular el vértice de una función cuadrática puede ser útil para maximizar ganancias, minimizar costos o encontrar puntos de equilibrio.

Además, el vértice también nos proporciona información sobre los puntos de intersección de la parábola con los ejes x e y. En el caso del vértice con las coordenadas (h, k), la x del vértice indica el punto donde la parábola corta al eje x, mientras que la y del vértice nos da el valor mínimo o máximo de la función. Estos puntos de intersección pueden tener aplicaciones prácticas en diversas áreas, como la arquitectura, la ingeniería civil o el diseño gráfico.

Calcular el vértice de una parábola solía ser una tarea compleja y laboriosa, pero gracias a las fórmulas existentes, podemos hacerlo de manera rápida y sencilla. ¡Ya no es necesario depender de cálculos manuales o extensos procesos algebraicos! A continuación, te enseñaremos una fórmula infalible para calcular el vértice de una parábola en cuestión de segundos.

La fórmula del vértice

La fórmula del vértice nos permite encontrar las coordenadas (h, k) del vértice de una parábola definida por la función cuadrática f(x) = ax² + bx + c. Esta fórmula se obtiene a partir de la forma general de la función cuadrática, conocida como forma canónica o forma completa, que se expresa como f(x) = a(x - h)² + k. En esta forma, (h, k) representa las coordenadas del vértice.

Para hallar las coordenadas del vértice, necesitamos conocer los valores de los coeficientes a, b y c de la función cuadrática. Una vez que los tengamos, podemos utilizar la siguiente fórmula:


h = -b / (2a)
k = f(h) = ah² + bh + c


En la primera ecuación, dividimos el opuesto de b entre 2a para obtener el valor de h. Esto nos da la coordenada x del vértice. Luego, substituimos este valor de h en la función cuadrática para calcular el valor de y o k. De esta manera, obtenemos las coordenadas completas del vértice (h, k).

Cuál es la fórmula utilizada para calcular el vértice de una parábola

Calcular el vértice de una parábola es una tarea fundamental en matemáticas y puede ser útil en una variedad de aplicaciones. Existe una fórmula específica que nos permite encontrar fácilmente las coordenadas del vértice de una parábola, ya sea que estemos trabajando con una parábola que abre hacia arriba o una que abre hacia abajo.

Fórmula para la parábola que abre hacia arriba

Si tenemos una parábola de la forma y = ax^2 + bx + c que abre hacia arriba, podemos utilizar la siguiente fórmula para calcular las coordenadas del vértice:

• Coordenada x del vértice: x = -b / (2a)
• Coordenada y del vértice: y = -(b^2 - 4ac) / (4a)

La fórmula nos indica que para encontrar la coordenada x del vértice, debemos tomar el opuesto del coeficiente lineal dividido por el doble del coeficiente cuadrático. Para encontrar la coordenada y, tomamos el opuesto de la ecuación discriminante (b^2 - 4ac) dividido por cuatro veces el coeficiente cuadrático.

Una vez que tenemos estas coordenadas, podemos representar el vértice de la parábola en un plano cartesiano, lo que nos dará información valiosa sobre la ubicación y la forma de la parábola.

Fórmula para la parábola que abre hacia abajo

Si estamos trabajando con una parábola que abre hacia abajo, la fórmula para calcular el vértice es similar, pero con algunos cambios:

• Coordenada x del vértice: x = -b / (2a)
• Coordenada y del vértice: y = -(b^2 + 4ac) / (4a)

Aquí, nuevamente tomamos el opuesto del coeficiente lineal dividido por el doble del coeficiente cuadrático para encontrar la coordenada x. Para la coordenada y, tomamos el opuesto de la suma del cuadrado del coeficiente lineal y cuatro veces el producto de los coeficientes cuadrático y constante.

Esta fórmula nos permite obtener de manera rápida y precisa las coordenadas del vértice de cualquier tipo de parábola, ya sea que abra hacia arriba o hacia abajo. Al utilizar estos cálculos en diferentes contextos, podemos tomar decisiones informadas, resolver problemas y comprender mejor las características de las parábolas.

Cuáles son los pasos para utilizar la fórmula del vértice y calcularlo rápidamente

El vértice de una parábola es un punto crucial que nos brinda información valiosa sobre su forma y posición en el plano cartesiano. Calcular este punto puede resultar intimidante al principio, pero con la fórmula adecuada y un poco de práctica, puedes dominar este proceso en cuestión de segundos.

Paso 1: Identificar los coeficientes

Antes de utilizar la fórmula del vértice, debemos identificar los coeficientes de la ecuación de la parábola en su forma estándar (y = ax² + bx + c). El coeficiente "a" es el factor que multiplica a x², el coeficiente "b" multiplica a x y el coeficiente "c" representa el término independiente.

Paso 2: Determinar las coordenadas x e y del vértice

Una vez que tenemos los coeficientes, podemos utilizar la siguiente fórmula para calcular las coordenadas x e y del vértice:

x = -b/2a

Para obtener el valor de "x", simplemente reemplazamos los coeficientes en la fórmula. Una vez que obtenemos el valor de "x", lo substituimos nuevamente en la ecuación de la parábola para encontrar el valor de "y".

Paso 3: Graficar el vértice

Una vez que hemos calculado las coordenadas x e y del vértice, podemos proceder a graficarlo en el plano cartesiano. La coordenada x representa la posición horizontal del vértice y la coordenada y representa su posición vertical.

Es importante notar que el vértice siempre se encuentra en una posición crítica de la parábola, ya sea un punto máximo o mínimo, dependiendo del valor del coeficiente "a". Si "a" es positiva, el vértice estará en el punto más bajo (mínimo) de la parábola. Por otro lado, si "a" es negativa, el vértice estará en el punto más alto (máximo) de la parábola.

Paso 4: Aplicar la fórmula en ejemplos prácticos

La mejor manera de comprender completamente la fórmula del vértice es a través de ejemplos prácticos. A continuación, te proporcionaré algunos ejercicios y sus soluciones paso a paso para que puedas practicar y afianzar tus habilidades en el cálculo del vértice de una parábola.

• Ejercicio 1:

Determine el vértice de la parábola y = 2x² + 4x - 3.

• Ejercicio 2:

Hallar el vértice de la parábola y = -3x² + 6x + 2.

• Ejercicio 3:

Encuentre el vértice de la parábola y = x² - 8x + 16.

Recuerda practicar con diferentes ejemplos para fortalecer tus habilidades y familiarizarte con la fórmula del vértice. Una vez que domines este proceso, podrás calcular el vértice de una parábola en cuestión de segundos y aplicar esta información para resolver problemas más complejos en matemáticas y otros campos relacionados.

Qué información necesito saber previamente para calcular el vértice de una parábola

Antes de sumergirnos en cómo calcular el vértice de una parábola de forma rápida y precisa, es importante tener claro qué información necesitamos saber previamente. Esto nos ayudará a entender mejor el proceso y a asegurarnos de que estamos utilizando los datos correctos.

En primer lugar, debemos conocer la ecuación de la parábola. La forma general de una ecuación cuadrática (parábola) es y = ax^2 + bx + c, donde a, b y c son constantes conocidas. Es vital asegurarse de que nuestra ecuación esté escrita en esta forma antes de continuar. Si no lo está, tendremos que manipularla utilizando técnicas algebraicas para llegar a esta expresión estándar.

Otra información necesaria es si la parábola se abre hacia arriba o hacia abajo. Esto puede estar determinado por el coeficiente principal a. Si a es positivo, la parábola se abrirá hacia arriba, mientras que si a es negativo, la parábola se abrirá hacia abajo.

Finalmente, también necesitaremos conocer el vértice de la parábola como punto de referencia. El vértice tiene las coordenadas (h, k) y será crucial para nuestro cálculo. Dependiendo de la forma en que se nos presente la ecuación de la parábola, podemos obtener fácilmente el vértice, o en otros casos, tendremos que hacer algunos pasos adicionales para encontrarlo.

Ahora que sabemos qué información necesitamos previamente, podemos continuar y aprender cómo calcular el vértice de una parábola de manera rápida y eficiente. Con esta fórmula infalible, estarás calculando el vértice en cuestión de segundos. ¡Sigue leyendo para descubrirlo!

Cómo puedo identificar si una parábola tiene su vértice hacia arriba o hacia abajo

Para identificar si una parábola tiene su vértice hacia arriba o hacia abajo, es necesario analizar el coeficiente que acompaña a la variable cuadrática en la ecuación de la parábola. La forma general de una ecuación de una parábola es:

y = ax^2 + bx + c

Donde "a", "b" y "c" son coeficientes reales y "x" representa la variable independiente.

Si el coeficiente "a" es positivo, entonces la parábola abrirá hacia arriba y su vértice estará ubicado en el punto más bajo de la curva. Por ejemplo, consideremos la siguiente ecuación:

y = 2x^2 + 4x - 3

En este caso, el coeficiente "a" es igual a 2, que es positivo. Por lo tanto, la parábola abre hacia arriba y su vértice estará ubicado en el punto más bajo de la curva.

Por otro lado, si el coeficiente "a" es negativo, la parábola abrirá hacia abajo y su vértice estará ubicado en el punto más alto de la curva. Consideremos la siguiente ecuación:

y = -3x^2 + 6x + 2

Aquí, el coeficiente "a" es igual a -3, que es negativo. Por lo tanto, la parábola abre hacia abajo y su vértice estará ubicado en el punto más alto de la curva.

Con base en esta información, podemos determinar si una parábola tiene su vértice hacia arriba o hacia abajo analizando el coeficiente "a" en la ecuación de la parábola. Esto nos permite visualizar y comprender mejor la forma y orientación de la parábola, lo cual es fundamental al momento de calcular su vértice.

Hay alguna forma más sencilla de calcular el vértice de una parábola sin usar la fórmula

Calcular el vértice de una parábola puede parecer un proceso complicado y tedioso, especialmente si se utiliza la fórmula tradicional. Sin embargo, existe una forma mucho más sencilla de obtener este valor clave en cuestión de segundos sin tener que hacer largos cálculos matemáticos.

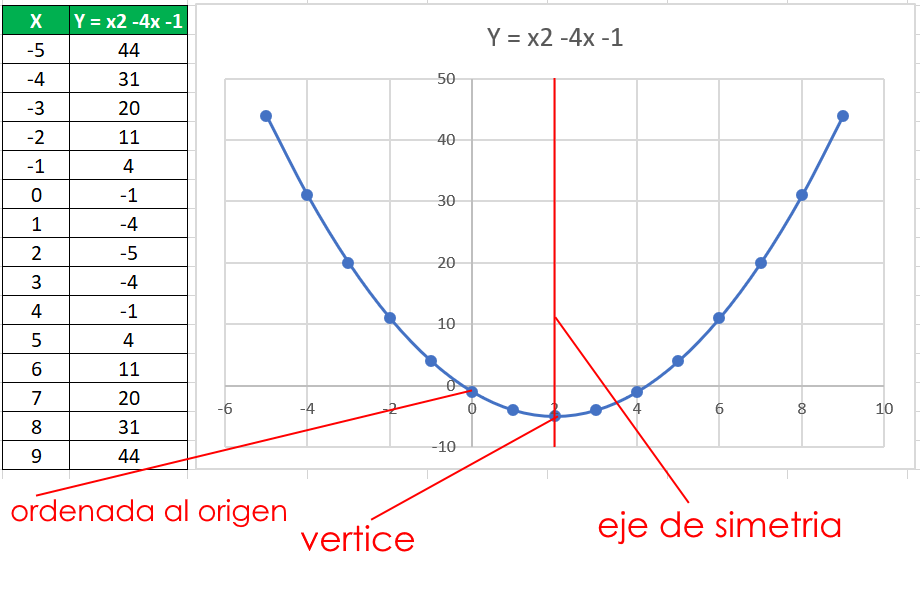
El truco está en utilizar la simetría de la parábola:

Antes de explicar cómo calcular el vértice de una parábola utilizando este método más simple y rápido, es importante comprender algunos conceptos básicos sobre las parábolas. Las parábolas son una de las formas más comunes de funciones cuadráticas y se caracterizan por tener una curva suave y simétrica.

La simetría de una parábola implica que tiene un eje de simetría vertical, que es una línea imaginaria que divide la parábola en dos partes iguales. Esta línea atraviesa el vértice de la parábola.

Entonces, ¿cómo podemos aprovechar esta simetría para calcular el vértice de una parábola de manera rápida y sencilla? La respuesta está en encontrar el punto que se encuentra justo en el medio entre los dos puntos de la parábola que están a la misma distancia del eje de simetría.

Sigue estos pasos para encontrar el vértice utilizando la simetría de la parábola:

1. Identifica el coeficiente principal de la función cuadrática, que generalmente se denota como "a".
2. Encuentra el eje de simetría de la parábola, que se define como "x = -b/2a", donde "b" es el coeficiente lineal.
3. Encuentra el punto de la parábola que cumple con la condición de simetría. Esto se puede hacer calculando dos puntos equidistantes del eje de simetría.
4. Calcula el promedio de las coordenadas x de estos dos puntos. Esto te dará la coordenada x del vértice.
5. Sustituye la coordenada x del vértice en la función cuadrática para calcular la coordenada y del vértice.
6. Listo, ¡has encontrado el vértice de la parábola utilizando la simetría!

Este método simplificado no solo ahorra tiempo, sino que también ayuda a tener una comprensión más intuitiva de la ubicación y forma del vértice de la parábola. Además, es una excelente manera de verificar cualquier cálculo anterior realizado con la fórmula tradicional.

Calcular el vértice de una parábola puede ser mucho más sencillo utilizando la simetría de la parábola. Al aprovechar la naturaleza simétrica de esta curva suave, podemos encontrar rápidamente el punto que representa el vértice sin necesidad de realizar complicados cálculos matemáticos. Así que la próxima vez que te enfrentes al desafío de encontrar el vértice de una parábola, recuerda este truco infalible y sorprende a todos con tu rapidez y precisión.

Qué aplicaciones prácticas tiene el cálculo del vértice de una parábola en la vida cotidiana

El cálculo del vértice de una parábola es una habilidad matemática fundamental que tiene muchas aplicaciones prácticas en la vida cotidiana. Aunque puede parecer un concepto abstracto, entender cómo calcular el vértice de una parábola puede ayudarnos a resolver una variedad de problemas en diferentes áreas.

Una de las aplicaciones más comunes de este cálculo se encuentra en el campo de la física. Por ejemplo, al estudiar la trayectoria de un proyectil en movimiento, como una pelota lanzada al aire o un cohete en vuelo, necesitamos conocer el punto más alto de dicha trayectoria, que corresponde justamente al vértice de la parábola que describe esa curva. Este conocimiento nos permite determinar la distancia máxima alcanzada, la altura máxima o el tiempo necesario para realizar cierto recorrido.

Otra aplicación práctica del cálculo del vértice de una parábola se encuentra en el ámbito financiero y económico. Las curvas de oferta y demanda, por ejemplo, pueden representarse mediante una parábola y encontrar su vértice es clave para determinar el equilibrio de mercado, donde la cantidad demandada se iguala a la cantidad ofrecida. Con esta información, se pueden tomar decisiones financieras más informadas y predecir los posibles cambios de precio y cantidad en el mercado.

En el ámbito de la arquitectura y el diseño, el cálculo del vértice de una parábola también juega un papel importante. Al diseñar estructuras como puentes, arcos o edificios con forma curva, el vértice de la parábola puede ayudar a determinar la forma óptima y la ubicación de los elementos estructurales principales, garantizando una mayor resistencia y estabilidad.

Por otro lado, en el campo de la educación, comprender y ser capaz de calcular el vértice de una parábola puede ayudar a los estudiantes a desarrollar habilidades de razonamiento lógico y abstracto. Esta habilidad matemática también puede ser aplicada en otros campos científicos, como la estadística y la investigación de datos, donde el análisis de diferentes relaciones y tendencias se basa en la identificación de patrones y puntos críticos como el vértice de una parábola.

El cálculo del vértice de una parábola tiene diversas aplicaciones prácticas que van desde la física y la economía hasta la arquitectura y la educación. Conocer cómo encontrar este punto crítico nos permite resolver problemas de manera más eficiente y tomar decisiones informadas en diferentes áreas de nuestras vidas. Por lo tanto, dedicar tiempo a comprender y dominar este concepto matemático sin duda vale la pena.

Cuáles son algunos ejemplos y ejercicios para practicar el cálculo del vértice de una parábola

El cálculo del vértice de una parábola es fundamental en el estudio de las matemáticas y tiene diversas aplicaciones en campos como la física, la ingeniería y la economía. Aunque puede parecer complicado al principio, existen fórmulas y métodos infalibles para determinar con precisión las coordenadas del vértice de cualquier parábola.

Para poder practicar y mejorar tus habilidades en este tema, te presentamos algunos ejemplos y ejercicios para que puedas poner a prueba tus conocimientos:

Ejemplo 1:

Dada la función cuadrática f(x) = x^2 - 4x + 5, queremos calcular las coordenadas del vértice de la parábola asociada a esta función.

Para encontrar el vértice, primero necesitamos identificar los coeficientes de la función, en este caso a = 1, b = -4 y c = 5.

Ahora, utilizaremos la fórmula del vértice: x = -b / (2a) y y = f(x). Sustituyendo los valores correspondientes, obtenemos:

x = -(-4) / (2 * 1) = 2
y = f(2) = (2)^2 - 4(2) + 5 = 1

Por lo tanto, el vértice de la parábola es (2, 1).

Ejercicio 1:

Calcula las coordenadas del vértice de la parábola asociada a la función cuadrática f(x) = 2x^2 + 8x - 3.

Para resolver este ejercicio, debemos identificar los coeficientes de la función: a = 2, b = 8 y c = -3.

Sustituyendo estos valores en la fórmula del vértice, obtenemos:

x = -b / (2a) = -8 / (2 * 2) = -1
y = f(-1) = 2(-1)^2 + 8(-1) - 3 = -7

Así, el vértice de la parábola es (-1, -7).

Ejemplo 2:

Considera la función cuadrática f(x) = -3x^2 + 6x - 2. Vamos a determinar las coordenadas del vértice.

Una vez más, identificamos los coeficientes de la función: a = -3, b = 6 y c = -2.

Aplicando la fórmula para el vértice, tenemos:

x = -b / (2a) = -6 / (2 * -3) = 1
y = f(1) = -3(1)^2 + 6(1) - 2 = 1

Por lo tanto, el vértice de la parábola es (1, 1).

Ejercicio 2:

Determina las coordenadas del vértice de la parábola asociada a la función cuadrática f(x) = x^2 + 4x + 2.

Identificamos los coeficientes de la función: a = 1, b = 4 y c = 2.

Al aplicar la fórmula para el vértice, obtenemos:

x = -b / (2a) = -4 / (2 * 1) = -2
y = f(-2) = (-2)^2 + 4(-2) + 2 = -2

El vértice de la parábola es (-2, -2).

A través de estos ejemplos y ejercicios, podrás adquirir experiencia en el cálculo del vértice de una parábola y mejorar tus habilidades. Recuerda siempre identificar los coeficientes de la función y utilizar la fórmula correspondiente para obtener las coordenadas del vértice. ¡Practica con diferentes ejercicios y desafíos para dominar este concepto fundamental de las matemáticas!

Existen recursos en línea o aplicaciones que pueden ayudar a calcular el vértice de una parábola de manera rápida y precisa

Calcular el vértice de una parábola puede ser un proceso complicado y consumir mucho tiempo si se realiza manualmente. Sin embargo, gracias a los avances tecnológicos y los recursos en línea disponibles actualmente, este cálculo puede realizarse en cuestión de segundos.

Una opción popular para calcular el vértice de una parábola es utilizar una aplicación o programa en línea. Estas herramientas simplifican el proceso al proporcionar campos de entrada donde puedes ingresar los coeficientes de la ecuación cuadrática que representa la parábola. A continuación, la aplicación realiza los cálculos necesarios y muestra los resultados de manera instantánea.

Además de las aplicaciones en línea, también existen sitios web que ofrecen calculadoras especializadas para encontrar el vértice de una parábola. Estas calculadoras suelen ser intuitivas y fáciles de usar, lo que las convierte en una excelente opción tanto para estudiantes como para profesionales.

¿Cómo funcionan estas soluciones en línea?

Las aplicaciones y calculadoras en línea utilizan la fórmula general de la ecuación cuadrática para determinar el vértice de una parábola. Esta fórmula es:

x = -b / (2a)

Donde a y b son los coeficientes de la ecuación cuadrática. Al ingresar estos valores en la aplicación o calculadora en línea, el programa realiza los cálculos necesarios y arroja el resultado.

Es importante destacar que estas herramientas no solo calculan el vértice de una parábola, sino que también proporcionan información adicional, como las coordenadas del vértice y la concavidad de la parábola. Esto hace que estas soluciones en línea sean aún más útiles y completas.

Ventajas de utilizar recursos en línea para calcular el vértice de una parábola

1. Ahorro de tiempo: Con una calculadora en línea, es posible obtener los resultados deseados en cuestión de segundos. Esto permite realizar cálculos rápidos y eficientes, sin tener que dedicar demasiado tiempo a la tarea.

2. Precisión: Las aplicaciones y calculadoras en línea utilizan algoritmos precisos para realizar los cálculos. Esto garantiza la exactitud de los resultados y evita posibles errores humanos al realizar los cálculos manualmente.

3. Accesibilidad: Estas soluciones en línea están disponibles en cualquier momento y lugar, siempre y cuando se tenga acceso a Internet. Esto significa que puedes calcular el vértice de una parábola desde tu computadora, tableta o incluso tu smartphone.

Si necesitas calcular el vértice de una parábola de manera rápida y precisa, no dudes en recurrir a los recursos en línea disponibles. Estas aplicaciones y calculadoras simplificarán el proceso y te proporcionarán resultados confiables en tan solo unos segundos.

El vértice de una parábola es el punto más alto o más bajo de la curva, dependiendo de si la parábola se abre hacia arriba o hacia abajo.

El vértice de una parábola se puede calcular utilizando la fórmula (-b/2a, f(-b/2a)), donde a, b y c son los coeficientes de la ecuación cuadrática.

El vértice de una parábola nos da información sobre el máximo o mínimo de la función. Además, podemos utilizarlo para encontrar el eje de simetría de la parábola.

Si el coeficiente a de la ecuación cuadrática es positivo, el vértice estará en un mínimo. Si el coeficiente a es negativo, el vértice estará en un máximo.

Para graficar el vértice de una parábola, trazamos una línea vertical que pase por el punto (h, k), donde h es la coordenada x del vértice y k es la coordenada y del vértice.