Jerarquía de Operaciones: Descubre cómo realizar cálculos matemáticos de manera efectiva

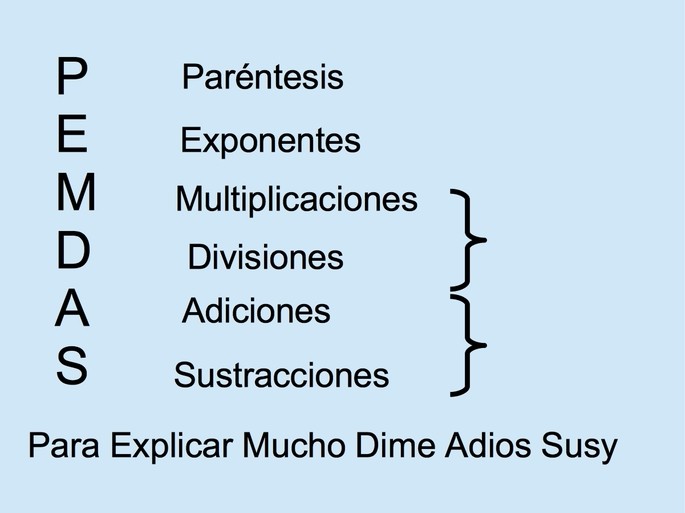
La jerarquía de operaciones, también conocida como regla de precedencia, es un conjunto de reglas que se utilizan para determinar el orden correcto en el que se deben realizar las operaciones matemáticas. Estas reglas son fundamentales para evitar ambigüedades y obtener resultados precisos en nuestros cálculos.

Exploraremos las diferentes operaciones matemáticas y su jerarquía, desde las más básicas como la suma y resta, hasta las operaciones más complejas como las exponenciales y las raíces cuadradas. Además, veremos ejemplos prácticos que nos ayudarán a comprender mejor cómo aplicar correctamente la jerarquía de operaciones en distintos escenarios. Aprender estas reglas nos permitirá realizar cálculos de manera efectiva y eficiente, optimizando nuestros resultados en el campo de las matemáticas.

Qué es la jerarquía de operaciones en matemáticas y por qué es importante entenderla

La jerarquía de operaciones en matemáticas es un conjunto de reglas que establece el orden en el que se deben realizar las operaciones matemáticas cuando nos encontramos con una expresión o ecuación que involucra múltiples operaciones. Estas reglas nos indican cuál es la operación que debemos realizar primero, cuál debe ser la siguiente y así sucesivamente, de manera que podamos obtener el resultado correcto.

La jerarquía de operaciones se basa en el principio de que algunas operaciones son más prioritarias que otras. Esto significa que hay ciertas operaciones que deben hacerse antes que otras, para garantizar la precisión y coherencia de los resultados. Si no seguimos la jerarquía de operaciones y realizamos las operaciones en cualquier orden, podemos obtener respuestas erróneas e incorrectas.

Las operaciones básicas en la jerarquía

En la jerarquía de operaciones, existen cuatro operaciones básicas que debemos tener en cuenta: suma, resta, multiplicación y división. Estas operaciones se destacan como las operaciones fundamentales de las matemáticas y forman la base de todos los cálculos numéricos.

La multiplicación y la división tienen mayor prioridad que la suma y la resta. Esto significa que las operaciones de multiplicación y división se deben realizar antes que las operaciones de suma y resta cuando aparecen juntas en una expresión.

Uso de paréntesis en la jerarquía de operaciones

Otro aspecto importante en la jerarquía de operaciones es el uso de paréntesis. Los paréntesis se utilizan para indicar que las operaciones contenidas dentro de ellos deben realizarse en primer lugar, incluso si no siguen la jerarquía establecida.

Al usar paréntesis, estamos agrupando ciertas operaciones y diciéndole a nuestra calculadora (o a nosotros mismos) que debe realizar esas operaciones antes que las demás. Este mecanismo resulta muy útil cuando queremos dar prioridad a ciertos cálculos y asegurarnos de que se realicen primero.

Ejemplo práctico de la jerarquía de operaciones

Para comprender mejor cómo funciona la jerarquía de operaciones, consideremos el siguiente ejemplo:

(4 + 2) x 3 - 5

De acuerdo con la jerarquía de operaciones, debemos resolver primero los paréntesis, luego realizar la multiplicación y, por último, la resta. Aplicando esto al ejemplo anterior, tenemos:

(6) x 3 - 5

Luego, realizamos la multiplicación:

18 - 5

Y finalmente, hacemos la resta:

13

Por lo tanto, el resultado de la expresión es 13.

Este ejemplo ilustra claramente cómo seguir la jerarquía de operaciones nos permite obtener el resultado correcto. Si hubiéramos realizado las operaciones en un orden distinto, habríamos obtenido una respuesta incorrecta.

Comprender y aplicar la jerarquía de operaciones en matemáticas es fundamental para realizar cálculos de manera efectiva y obtener resultados precisos. Siguiendo las reglas establecidas y prestando atención al orden de las operaciones, podemos evitar errores y asegurar la coherencia en nuestros cálculos numéricos.

Cuáles son los diferentes niveles de la jerarquía de operaciones y en qué orden deben ser ejecutados

La jerarquía de operaciones, también conocida como regla de precedencia de operaciones, es un conjunto de reglas que determinan el orden en que se deben realizar las operaciones matemáticas en una expresión numérica. Esta jerarquía asegura que los cálculos se realicen de manera correcta y efectiva.

En la jerarquía de operaciones existen diferentes niveles o categorías de operaciones, y cada una tiene un nivel de precedencia definido. Estos niveles son:

Nivel 1: Paréntesis y otros símbolos de agrupación

En este primer nivel, todas las operaciones dentro de paréntesis deben realizarse primero. Esto incluye cualquier operación que esté dentro de paréntesis (), corchetes , llaves {}, así como cualquier otro símbolo de agrupación específico. Dentro de estos grupos, se puede aplicar nuevamente la jerarquía de operaciones para determinar el orden correcto de las operaciones.

Nivel 2: Exponentes y raíces cuadradas

En el segundo nivel se encuentran las operaciones de exponentes y raíces cuadradas. Si la expresión contiene alguna operación con exponentes, se deben resolver antes que cualquier otra operación. Las raíces cuadradas también se deben calcular en este nivel.

Nivel 3: Multiplicación y división

En el tercer nivel se encuentran las operaciones de multiplicación y división. Estas operaciones se deben realizar de izquierda a derecha, siguiendo el orden en que se presentan en la expresión. Si la expresión contiene múltiples operaciones de multiplicación o división, se deben resolver en el orden en que aparecen.

Nivel 4: Suma y resta

En el último nivel se encuentran las operaciones de suma y resta. Al igual que las operaciones de multiplicación y división, se deben realizar de izquierda a derecha, siguiendo el orden en que se presentan en la expresión. Si la expresión contiene múltiples operaciones de suma o resta, se deben resolver en el orden en que aparecen.

El uso de paréntesis puede alterar el orden de ejecución de las operaciones dentro de una expresión. Si hay paréntesis anidados, los cálculos se realizan en orden de profundidad, es decir, primero los más internos y luego los más externos.

Es importante tener en cuenta que dentro de un mismo nivel de la jerarquía de operaciones, las operaciones se resuelven de izquierda a derecha.

A continuación se muestra un ejemplo aplicando la jerarquía de operaciones:


2 + 3 * (4 - 1) / 2


Aplicando la jerarquía de operaciones, primero se resuelve la operación dentro del paréntesis:


2 + 3 * 3 / 2


Luego se realiza la multiplicación y la división:


2 + 9 / 2


Finalmente, se realiza la suma:


2 + 4.5 = 6.5


Seguir correctamente la jerarquía de operaciones es fundamental para obtener resultados precisos y evitar confusiones en nuestros cálculos matemáticos.

Cómo se realiza la operación de paréntesis y cuál es su importancia en la jerarquía de operaciones

En la jerarquía de operaciones matemáticas, una de las primeras reglas es resolver las operaciones dentro de paréntesis antes que cualquier otra. Los paréntesis tienen una gran importancia en la forma en que se llevan a cabo los cálculos y pueden cambiar significativamente el resultado final.

Los paréntesis nos permiten agrupar ciertas operaciones y asegurarnos de que se realicen en primer lugar. Esto es especialmente útil cuando tenemos expresiones matemáticas más largas y complicadas, ya que nos permite evitar errores y confusiones al momento de hacer los cálculos.

Cuando se presentan paréntesis, debemos comenzar por resolver todas las operaciones que estén dentro de ellos. Esto significa que cualquier suma, resta, multiplicación o división que se encuentre dentro del paréntesis debe ser resuelta primero.

Ejemplo:

Si tenemos la expresión matemática (4 + 2) * 3, siguiendo la jerarquía de operaciones, primero debemos sumar 4 y 2, lo cual nos da un resultado de 6. Luego, multiplicamos ese resultado por 3, obteniendo un resultado final de 18.

Es importante mencionar que si hay más de un conjunto de paréntesis, debemos resolverlos teniendo en cuenta el orden en el que aparecen. Si hay paréntesis anidados, es decir, paréntesis dentro de otros paréntesis, debemos resolver primero los más internos y luego ir avanzando hacia los más externos.

También es relevante destacar que los paréntesis pueden cambiar por completo el resultado de una expresión matemática. Por ejemplo, si tenemos la expresión 5 * (4 + 2), el resultado será 30, ya que primero se realiza la suma dentro del paréntesis y luego se multiplica el resultado por 5.

Los paréntesis son fundamentales en la jerarquía de operaciones matemáticas, ya que nos permiten especificar qué operaciones deben ser resueltas en primer lugar. Son una herramienta poderosa para organizar y simplificar cálculos más complejos, evitando errores y garantizando resultados precisos.

Cuál es el papel de los exponentes y las raíces en la jerarquía de operaciones

En la jerarquía de operaciones, los exponentes y las raíces juegan un papel fundamental en el orden de los cálculos matemáticos. Estas operaciones permiten expresar de manera concisa y efectiva números grandes o pequeños, así como calcular el valor de una incógnita a partir de una ecuación.

Exponentes

Los exponentes son utilizados para representar la multiplicación repetida de un número por sí mismo. Se les suele llamar potencias, y se representan mediante un número base elevado a una potencia. Por ejemplo, 2^3 significa que se debe multiplicar el número 2 por sí mismo 3 veces: 2 * 2 * 2 = 8.

Al utilizar los exponentes, podemos simplificar y resolver expresiones matemáticas de manera más eficiente. Esto es especialmente útil en casos donde se requiere realizar operaciones con números grandes, como en la física o en la economía.

Raíces

Las raíces, por otro lado, son operaciones inversas a los exponentes. La raíz n-ésima de un número es aquel valor que, al elevarlo a la potencia de n, nos da como resultado el número original. Se representa mediante el símbolo radical (√).

Por ejemplo, la raíz cuadrada de 9 (√9) es igual a 3, ya que 3^2 = 9. De manera similar, la raíz cúbica de 27 (∛27) es igual a 3, ya que 3^3 = 27.

Las raíces son utilizadas para calcular valores desconocidos o soluciones de ecuaciones. Son particularmente importantes en el álgebra y la geometría, donde nos permiten determinar longitudes, áreas y volúmenes.

Jerarquía de operaciones

Los exponentes y las raíces son operaciones claves dentro de la jerarquía de operaciones matemáticas. Estas nos permiten simplificar cálculos, resolver ecuaciones y representar números grandes o pequeños de manera eficiente.

Es importante recordar que en la jerarquía de operaciones, primero se realizan las operaciones dentro de los paréntesis, luego las potencias y raíces, seguidas de las multiplicaciones y divisiones, y por último, las sumas y restas.

Al comprender y aplicar correctamente la jerarquía de operaciones, podemos realizar cálculos matemáticos de manera efectiva y obtener resultados precisos.

Qué son las multiplicaciones y divisiones y cómo se realizan dentro de la jerarquía de operaciones

Las multiplicaciones y divisiones son operaciones fundamentales en matemáticas y se realizan dentro de la jerarquía de operaciones. La jerarquía de operaciones establece el orden en el que deben realizarse diferentes operaciones matemáticas cuando aparecen juntas en una expresión. Siguiendo correctamente esta jerarquía, podemos resolver cálculos de manera efectiva y obtener resultados precisos.

La multiplicación es una operación que combina dos o más números para obtener un producto. Se denota con el símbolo "x" o el punto ".". Dentro de la jerarquía de operaciones, la multiplicación se realiza antes que la suma y la resta. Esto significa que si tenemos una expresión que contiene tanto multiplicaciones como sumas o restas, primero debemos realizar las multiplicaciones antes de continuar con las otras operaciones.

Por ejemplo, si tenemos la expresión matemática 3 + 4 x 2, según la jerarquía de operaciones, debemos realizar la multiplicación antes que la suma. Entonces, multiplicamos 4 por 2, obteniendo 8, y luego sumamos 3 a ese resultado, obteniendo finalmente 11.

En cuanto a la división, es otra operación básica que implica distribuir un número en partes iguales. Se denota con el símbolo de división "÷" o con el signo ":". Al igual que con la multiplicación, la jerarquía de operaciones dicta que la división se realice antes que la suma y la resta.

Supongamos que tenemos la expresión 10 - 5 ÷ 2. Según la jerarquía de operaciones, debemos realizar la división antes que la resta. Dividimos 5 por 2 y obtenemos 2.5, luego restamos ese resultado de 10, obteniendo finalmente 7.5.

Es importante recordar que dentro de la jerarquía de operaciones también se deben considerar los paréntesis. Las expresiones encerradas en paréntesis tienen prioridad sobre las demás operaciones. Si hay paréntesis dentro de multiplicaciones o divisiones, estas deben resolverse primero antes de continuar con el resto de la expresión.

Para realizar cálculos matemáticos de manera efectiva es necesario comprender y seguir la jerarquía de operaciones. Asegurarse de realizar las multiplicaciones y divisiones antes que las sumas y restas garantiza obtener resultados precisos. Además, es esencial prestar atención a los paréntesis y resolver primero las operaciones que están dentro de ellos. Con este conocimiento, podrás realizar cálculos matemáticos rápidamente y evitar errores.

Cuáles son los pasos para realizar sumas y restas correctamente siguiendo la jerarquía de operaciones

La jerarquía de operaciones es una regla fundamental en matemáticas que establece el orden en el que se deben realizar las operaciones en una expresión matemática para obtener el resultado correcto. Los cálculos matemáticos siguen una secuencia específica, y conocer esta jerarquía es esencial para realizar sumas y restas correctamente.

Para realizar sumas y restas correctamente siguiendo la jerarquía de operaciones, debemos seguir los siguientes pasos:

Paso 1: Resolver paréntesis

El primer paso consiste en resolver cualquier operación que se encuentre dentro de paréntesis. Es importante recordar que se deben resolver los paréntesis internos primero antes de los externos.

Ejemplo:

Si tenemos la expresión (3 + 2) - 4, primero resolvemos la suma dentro del paréntesis: 3 + 2 = 5. Luego, restamos 4 a ese resultado: 5 - 4 = 1.

Paso 2: Realizar multiplicaciones y divisiones

Una vez que hemos resuelto los paréntesis, procedemos a realizar las multiplicaciones y divisiones en la expresión. Estas operaciones se realizan de izquierda a derecha.

Ejemplo:

Si tenemos la expresión 3 + 2 * 4 / 2, primero realizamos la multiplicación: 2 * 4 = 8. Luego, la división: 8 / 2 = 4. Por último, sumamos 3 a ese resultado: 3 + 4 = 7.

Paso 3: Calcular sumas y restas

Finalmente, una vez que hemos resuelto las multiplicaciones y divisiones, procedemos a realizar las sumas y restas en la expresión. Estas operaciones también se realizan de izquierda a derecha.

Ejemplo:

Si tenemos la expresión 3 + 2 - 1 + 5, primero sumamos 3 + 2 = 5. Luego, restamos 1: 5 - 1 = 4. Por último, sumamos 4 a 5: 4 + 5 = 9.

Para realizar sumas y restas correctamente siguiendo la jerarquía de operaciones, debemos resolver primero los paréntesis, luego realizar las multiplicaciones y divisiones, y finalmente calcular las sumas y restas. Siguiendo estos pasos, podremos efectuar cálculos matemáticos de manera precisa y fiable.

Es posible saltarse la jerarquía de operaciones y realizar las operaciones en otro orden? ¿Por qué o por qué no

La jerarquía de operaciones es un principio fundamental en matemáticas que establece el orden en que se deben realizar las operaciones en una expresión matemática para obtener el resultado correcto. Este orden es conocido por todos: primero los paréntesis, luego las potencias y raíces, seguidas de la multiplicación y división, y finalmente la suma y resta.

A pesar de ser una regla ampliamente aceptada y utilizada, a menudo surge la pregunta de si es posible saltarse esta jerarquía y realizar las operaciones en otro orden. La respuesta sencilla es no, ya que hacerlo podría conducir a resultados incorrectos.

Para comprender mejor por qué no se puede saltar la jerarquía de operaciones, es importante entender cómo funciona cada uno de los elementos involucrados. Comenzando con los paréntesis, estos permiten agrupar ciertas partes de una expresión y calcularlas antes de continuar con el resto. Esto es crucial cuando hay diferentes operaciones en juego, ya que asegura que se realicen las operaciones internas antes de seguir adelante.

Las potencias y raíces, por su parte, son otra consideración importante. Estas operaciones se aplican después de los paréntesis y antes de la multiplicación, división, suma y resta. Ignorar este orden podría conducir a resultados incorrectos, ya que las potencias y raíces tienen prioridad sobre las demás operaciones.

Luego, llegamos a la multiplicación y división. Aunque estas operaciones son similares en términos de precedencia, se realizan de izquierda a derecha. Saltarse esta regla específica podría dar lugar a un resultado incorrecto si no se mantiene el orden establecido.

Finalmente, la suma y resta son las últimas operaciones que se realizan en la jerarquía de operaciones. Al igual que la multiplicación y la división, estas operaciones también se realizan de izquierda a derecha. Pasar por alto este orden podría desencadenar errores matemáticos y proporcionar resultados incorrectos.

La jerarquía de operaciones es un principio fundamental en matemáticas que establece el orden correcto en que se deben realizar las operaciones para obtener resultados precisos. No es posible saltarse esta regla sin consecuencias, ya que cada elemento tiene una prioridad específica y su orden debe ser respetado. Ignorar o alterar esta jerarquía puede llevar a cálculos erróneos y resultados incorrectos.

Qué consejos prácticos puedes seguir para recordar y aplicar correctamente la jerarquía de operaciones

La jerarquía de operaciones es una regla fundamental en matemáticas que establece el orden en el cual se deben realizar las diferentes operaciones matemáticas dentro de una expresión o ecuación. Seguir correctamente esta jerarquía es esencial para obtener resultados precisos y evitar errores en los cálculos.

A continuación, te presentaremos algunos consejos prácticos que te ayudarán a recordar y aplicar de manera efectiva la jerarquía de operaciones:

1. Paréntesis

Los paréntesis son la operación de mayor prioridad en la jerarquía. Las operaciones dentro de los paréntesis deben ser resueltas primero. Recuerda prestar atención a los diferentes niveles de paréntesis para resolverlos en el orden correcto.

2. Potencias y raíces

En segundo lugar, se resuelven las potencias y raíces. Calcula todas las potencias y raíces presentes en la expresión en el orden en el que aparecen.

3. Multiplicación y división

La multiplicación y la división tienen la misma prioridad y se resuelven de izquierda a derecha. Realiza estas operaciones en el orden en que aparecen en la expresión.

4. Suma y resta

Finalmente, la suma y la resta también tienen la misma prioridad y se resuelven de izquierda a derecha. Realiza estas operaciones en el orden en el que aparecen en la expresión.

Es importante mencionar que si una expresión contiene varias operaciones de la misma prioridad, se deben resolver siguiendo el orden en el que aparecen de izquierda a derecha. Esto garantiza la consistencia y exactitud en los cálculos.

Recuerda utilizar correctamente los paréntesis para agrupar las operaciones y así evitar confusiones o ambigüedades. Además, lleva un registro ordenado de tus cálculos para no perder el hilo y cometer errores.

Seguir adecuadamente la jerarquía de operaciones es fundamental para realizar cálculos matemáticos de manera efectiva. Recuerda resolver primero las operaciones dentro de los paréntesis, luego las potencias y raíces, seguidas de la multiplicación y división, y finalmente la suma y resta. Aplica estos consejos prácticos y disfruta de una mayor precisión en tus cálculos.

Cuál es la importancia de utilizar paréntesis adicionales para aclarar la interpretación de una expresión matemática según la jerarquía de operaciones

La jerarquía de operaciones es fundamental en matemáticas, ya que nos permite realizar cálculos de manera precisa y efectiva. Sin embargo, cuando nos enfrentamos a expresiones matemáticas complejas, es posible que necesitemos utilizar paréntesis adicionales para aclarar la interpretación de dichas expresiones.

Los paréntesis son utilizados para agrupar partes específicas de una expresión, estableciendo así un orden de ejecución dentro de la jerarquía de operaciones. La correcta colocación de paréntesis nos ayuda a evitar confusiones e interpretaciones erróneas al resolver una expresión.

Por ejemplo, consideremos la siguiente expresión: 2 + 3 * 4. Según la jerarquía de operaciones, la multiplicación debe realizarse antes de la suma. Por lo tanto, el resultado correcto sería 2 + (3 * 4) = 14. Si no utilizamos los paréntesis adicionales, podríamos interpretar la expresión de manera errónea y obtener un resultado incorrecto.

En algunos casos, también podemos encontrarnos con situaciones donde sea necesario utilizar múltiples niveles de paréntesis para aclarar aún más la interpretación de una expresión. Esto suele suceder cuando tenemos distintas operaciones combinadas en una misma expresión.

Por ejemplo, consideremos la siguiente expresión: 3 + 4 * 2 - 1. Una posible interpretación podría ser calcular primero la multiplicación y luego realizar las sumas y restas. Sin embargo, si queremos asegurarnos de seguir correctamente la jerarquía de operaciones, podríamos utilizar paréntesis adicionales de la siguiente manera: (3 + (4 * 2)) - 1. Esto nos permite realizar primero la multiplicación, luego la suma y finalmente la resta, obteniendo así un resultado correcto.

Utilizar paréntesis adicionales para aclarar la interpretación de una expresión matemática es fundamental cuando trabajamos con la jerarquía de operaciones. Los paréntesis nos permiten establecer un orden de ejecución preciso, evitando así confusiones y obteniendo resultados precisos y efectivos en nuestros cálculos matemáticos.

Hay casos especiales en los que es necesario seguir un orden específico dentro de cada nivel de la jerarquía de operaciones

La jerarquía de operaciones es fundamental en las matemáticas, ya que establece un orden específico en el que deben realizarse los cálculos. Este orden se aplica a expresiones numéricas o algebraicas que involucran diferentes operaciones matemáticas como la suma, resta, multiplicación, división, entre otras.

Es importante tener en cuenta que seguir correctamente la jerarquía de operaciones es crucial para obtener resultados precisos y evitar cualquier tipo de confusión o error en los cálculos. En algunos casos, existen situaciones especiales en las que es necesario seguir un orden específico dentro de cada nivel de la jerarquía.

Dentro del nivel de paréntesis

En primer lugar, cuando nos encontramos con una expresión que contiene paréntesis, debemos comenzar por resolver todas las operaciones que se encuentren en su interior. Esto incluye sumas, restas, multiplicaciones, divisiones e incluso otras operaciones más complejas.

Para esto podemos utilizar la regla mnemotécnica PEMDAS, que nos indica el orden en el que debemos realizar las operaciones dentro de los paréntesis: primero las potencias y radicales, luego las multiplicaciones y divisiones, y por último las sumas y restas.

Es importante recordar que si dentro de los paréntesis hay otro conjunto de ellos, debemos seguir el mismo proceso y resolver las operaciones dentro del paréntesis más interno primero.

Dentro del nivel de exponentes

Una vez que hayamos resuelto todas las operaciones dentro de los paréntesis, pasamos al siguiente nivel de la jerarquía, que son los exponentes. Aquí debemos calcular todas las potencias presentes en la expresión.

Si hay varios exponentes en una misma expresión, se deben calcular de izquierda a derecha. Es decir, primero resolvemos el exponente más a la izquierda y luego seguimos con los demás según el orden en que aparecen.

Dentro del nivel de multiplicaciones y divisiones

Una vez que hemos calculado todas las potencias, procedemos a resolver las operaciones de multiplicación y división que quedan en la expresión. Estas operaciones también se deben realizar de izquierda a derecha.

Si hay múltiples multiplicaciones y divisiones en una misma expresión, se debe dar prioridad a la que aparece primero y seguir en orden hasta terminar con todas ellas.

Dentro del nivel de sumas y restas

Por último, nos encontramos con el nivel de sumas y restas. Una vez que hayamos resuelto todas las operaciones anteriores, procedemos a realizar las sumas y restas que quedan en la expresión.

Al igual que en los niveles anteriores, si hay varias sumas y restas en una misma expresión, se deben calcular de izquierda a derecha, siguiendo el orden en que aparecen.

Es importante resaltar que si en algún momento nos encontramos con varios niveles de la jerarquía de operaciones dentro de una misma expresión, debemos seguir el orden establecido de manera secuencial, dando prioridad al nivel más alto antes de pasar al siguiente.

Entender y aplicar correctamente la jerarquía de operaciones es vital para realizar cálculos matemáticos de manera efectiva. Siguiendo el orden adecuado en cada nivel de la jerarquía, podemos obtener resultados precisos y evitar cualquier tipo de confusión o error al resolver expresiones numéricas o algebraicas.

Preguntas frecuentes (FAQ)

¿Cuál es la jerarquía de operaciones en matemáticas?

La jerarquía de operaciones establece el orden en el que debemos realizar las operaciones matemáticas: primero, paréntesis y corchetes; luego, potencias y raíces; después, multiplicación y división; por último, suma y resta.

¿Qué pasa si no sigo la jerarquía de operaciones?

Si no sigues la jerarquía de operaciones, puedes obtener resultados incorrectos en tus cálculos matemáticos. Los paréntesis y corchetes deben resolverse primero para evitar confusiones.

¿Qué es un exponente en matemáticas?

Un exponente es un número que indica cuántas veces se debe multiplicar una base por sí misma. Por ejemplo, en 2^3, 2 es la base y 3 es el exponente.

¿Qué son los paréntesis en una operación matemática?

Los paréntesis son símbolos utilizados para agrupar partes de una expresión matemática. Las operaciones dentro de los paréntesis deben realizarse primero según la jerarquía de operaciones.

¿Por qué es importante seguir la jerarquía de operaciones en matemáticas?

Es importante seguir la jerarquía de operaciones en matemáticas para obtener resultados precisos y evitar confusiones. Siguiendo el orden adecuado, aseguras que todas las operaciones sean realizadas correctamente.