Ubica una fracción en una recta numérica: Aprende cómo hacerlo de manera fácil y rápida

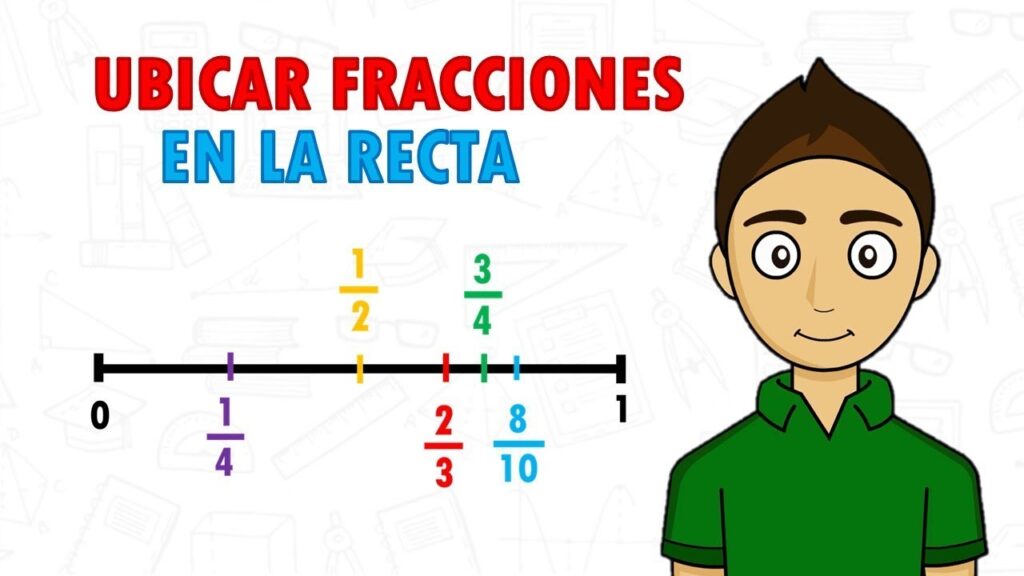
La representación gráfica de una fracción en una recta numérica es una herramienta útil para comprender mejor el valor relativo de una fracción en relación con otros números. Al colocar una fracción en una recta numérica, podemos visualizar dónde se ubica y compararla con otros valores numéricos.

Te enseñaremos paso a paso cómo ubicar una fracción en una recta numérica de manera fácil y rápida. Desde la identificación del denominador y numerador, hasta la elección adecuada de la escala de la recta numérica, aprenderás todo lo necesario para representar correctamente una fracción en una línea recta.

Qué es una recta numérica y para qué se utiliza

Una recta numérica es una representación gráfica de los números reales, dispuestos en una línea recta. Esta herramienta matemática nos permite visualizar y ubicar diferentes valores numéricos de manera ordenada y secuencial.

La recta numérica se compone de una línea horizontal donde se colocan los números, y cada punto de la línea representa un número específico. Los números negativos se ubican a la izquierda del cero, y los positivos a la derecha. El cero se sitúa en el centro de la recta numérica.

La utilidad de la recta numérica radica en que nos facilita la comprensión y el estudio de las operaciones matemáticas, así como la comparación y ubicación de fracciones, decimales y otros valores numéricos.

Cómo ubicar una fracción en una recta numérica

Para ubicar una fracción en una recta numérica, debemos seguir algunos pasos sencillos:

1. Identificar el denominador de la fracción. El denominador indica en cuántas partes se divide la unidad en la fracción.
2. Dibujar una línea recta horizontal y marcar en ella los valores numéricos necesarios, desde el mínimo hasta el máximo que abarque la fracción.
3. Dividir visualmente la recta en partes iguales según el denominador. Por ejemplo, si tenemos una fracción con denominador 4, dividiremos la recta en cuatro partes iguales.
4. Localizar la fracción en la recta. Si el numerador es mayor que 1, contaremos los segmentos desde el inicio de la recta. Si el numerador es igual a 1, ubicaremos el punto exactamente en el primer segmento que representa la fracción.

Por ejemplo, si queremos ubicar la fracción 3/4 en una recta numérica, seguiríamos estos pasos:

1. Dibujar una línea recta y marcar los valores necesarios, desde el mínimo hasta el máximo que abarque la fracción.
2. Dividir visualmente la recta en cuatro partes iguales.
3. Contar tres segmentos desde el inicio de la recta.
4. Ubicar un punto en el tercer segmento contado, que representará la fracción 3/4.

De esta manera, utilizando una recta numérica, podemos ubicar cualquier fracción de forma precisa y comprender mejor las relaciones numéricas.

Cómo se representan las fracciones en una recta numérica

La representación de las fracciones en una recta numérica es una herramienta útil para comprender la ubicación y relación de diferentes valores fraccionarios. Esta representación visual nos permite tener una mejor comprensión de cómo se relacionan las fracciones con respecto a los números enteros y otras fracciones.

Para ubicar una fracción en una recta numérica, primero debemos entender cómo funciona esta representación. Una recta numérica es una línea horizontal que se extiende infinitamente en ambas direcciones. En ella, cada punto representa un número real. Los puntos a la izquierda del cero representan números negativos, mientras que los puntos a la derecha del cero representan números positivos.

Para representar una fracción en una recta numérica, debemos considerar dos elementos importantes: el numerador y el denominador. El numerador representa la cantidad de partes que estamos tomando de la unidad entera, mientras que el denominador indica en cuántas partes se divide la unidad entera.

Paso 1: Determinar el rango de la recta numérica

Antes de comenzar a ubicar la fracción en la recta numérica, es importante determinar el rango que vamos a utilizar. Por ejemplo, si queremos representar fracciones entre 0 y 1, podemos utilizar una escala de 0 a 1 en nuestra recta numérica.

En este caso, divida la recta numérica en partes iguales que sean convenientes para representar la fracción que se va a ubicar. Por ejemplo, podríamos dividir la recta en 10 partes iguales o incluso en 100 partes iguales, dependiendo de la precisión que necesitemos.

Paso 2: Marcar la ubicación del numerador en la recta numérica

Una vez que hemos determinado el rango de nuestra recta numérica, procedemos a marcar la ubicación del numerador. Si el numerador es un número entero, simplemente lo ubicamos en el punto correspondiente en la recta numérica. Por ejemplo, si tenemos la fracción 3/4, ubicaremos el número 3 en el punto correspondiente.

Si el numerador es menor que el denominador, dividiremos una unidad en partes iguales y tomaremos el número de divisiones igual al numerador. Por ejemplo, para representar la fracción 1/4, dividiremos la unidad en 4 partes iguales y marcaremos la ubicación del primer segmento (el numerador) en la recta numérica.

Paso 3: Dividir la unidad en partes iguales

A continuación, debemos dividir la unidad en partes iguales según lo indique el denominador. Por ejemplo, si tenemos la fracción 3/4, dividiremos la unidad en 4 partes iguales.

Para hacer esto, utilizaremos las marcas ya realizadas en la recta numérica y añadiremos las divisiones restantes. Si ya habíamos marcado el numerador en el paso anterior, debemos asegurarnos de dividir las secciones restantes equitativamente.

Paso 4: Ubicar el numerador y trazar una línea

Finalmente, ubicamos el numerador en la recta numérica y trazamos una línea desde el cero hasta esa ubicación. Esta línea representa la fracción en la recta numérica.

Si tenemos una fracción mixta, es decir, una fracción que tiene un número entero más una fracción propia, primero ubicaremos el número entero en la recta numérica y luego representaremos la fracción propia siguiendo los pasos anteriores.

Una vez finalizados estos pasos, podemos visualizar fácilmente la ubicación de cualquier fracción en la recta numérica.

Cuál es el procedimiento paso a paso para ubicar una fracción en una recta numérica

Ubicar una fracción en una recta numérica puede parecer complicado al principio, pero con el procedimiento adecuado, puedes hacerlo de manera fácil y rápida. En este artículo te mostraremos paso a paso cómo realizar esta tarea de forma sencilla.

Paso 1: Identificar la fracción

Lo primero que debes hacer es identificar la fracción que deseas ubicar en la recta numérica. La fracción se compone de dos números: el numerador y el denominador. El numerador representa la cantidad de partes que queremos ubicar en la recta, mientras que el denominador indica en cuántas partes está dividida la unidad entera.

Paso 2: Establecer la escala de la recta

El siguiente paso es establecer la escala de la recta numérica. Para esto, debes determinar cuántos segmentos o divisiones quieres que tenga la recta. Esto dependerá del valor del denominador de la fracción. Si el denominador es 2, por ejemplo, podrías marcar la recta con dos segmentos iguales.

Paso 3: Marcar la ubicación del numerador en la recta

Una vez que has establecido la escala de la recta, es hora de marcar la ubicación del numerador. Si el numerador es igual a 1, simplemente marcas un punto en la recta en el primer segmento. Si el numerador es mayor que 1, cuentas los segmentos desde el inicio de la recta y marcas el punto correspondiente.

Paso 4: Conectar los puntos

Para tener una representación visual más clara, puedes conectar el punto que acabas de marcar con la línea recta que representa la recta numérica. Esto te ayudará a visualizar mejor la posición de la fracción en relación a los demás números.

Paso 5: Etiquetar otros puntos importantes

Si lo deseas, puedes etiquetar otros puntos importantes en la recta numérica. Por ejemplo, podrías marcar el punto correspondiente al valor de la mitad de la unidad entera, así como otros valores significativos para ti.

Paso 6: Verificar la ubicación de la fracción

Una vez que hayas seguido todos estos pasos, es importante verificar la ubicación de la fracción en la recta numérica. Observa si se encuentra en el lugar correcto de acuerdo al valor del numerador y denominador.

Ahora que conoces el procedimiento paso a paso para ubicar una fracción en una recta numérica, puedes practicar con diferentes ejemplos y perfeccionar tus habilidades en este tema. Recuerda que la práctica constante te permitirá dominar esta habilidad matemática de manera fácil y rápida.

Qué significa que una fracción esté más cerca del cero o del uno en una recta numérica

Una recta numérica es una línea recta que se utiliza para representar los números de manera ordenada y secuencial. Es una herramienta fundamental en matemáticas que nos permite visualizar y entender las relaciones entre los números.

Cuando hablamos de ubicar una fracción en una recta numérica, nos referimos a colocarla en el lugar correspondiente en la línea, de acuerdo a su valor. Para hacer esto, debemos entender qué significa que una fracción esté más cerca del cero o del uno en la recta numérica.

Imagina una recta numérica dibujada en un papel, que va desde el número cero hasta el número uno. En esta recta, el cero representa el punto de partida y el uno el punto final. Cada punto en la recta numérica representa un número específico, ya sea entero o fraccionario.

Al ubicar una fracción en la recta numérica, debemos fijarnos en dos cosas: el numerador y el denominador de la fracción. El numerador nos indica cuántas partes de la unidad estamos considerando, y el denominador nos dice en cuántas partes está dividida la unidad total.

Si el numerador es mayor al denominador, significa que la fracción está más cerca del uno en la recta numérica. Esto se debe a que estamos contemplando más partes de la unidad total. Por ejemplo, si tenemos la fracción 3/4, el numerador es mayor al denominador (3 es mayor a 4), lo que indica que estamos considerando tres partes de la unidad total de cuatro posibles. En la recta numérica, esta fracción estaría ubicada más cerca del uno que del cero.

Por otro lado, si el numerador es menor al denominador, la fracción estará más cerca del cero en la recta numérica. Esto se debe a que estamos considerando menos partes de la unidad total. Por ejemplo, si tenemos la fracción 1/5, el numerador es menor al denominador (1 es menor a 5), lo que indica que estamos considerando una parte de la unidad total de cinco posibles. En la recta numérica, esta fracción estaría ubicada más cerca del cero que del uno.

Es importante tener en cuenta que una fracción puede estar igualmente distante del cero y del uno en la recta numérica. En este caso, tanto el numerador como el denominador serían iguales, lo que indicaría que estamos considerando una cantidad igual de partes de la unidad total. Por ejemplo, si tenemos la fracción 1/2, el numerador es igual al denominador, lo que indica que estamos considerando una mitad de la unidad total. En la recta numérica, esta fracción estaría ubicada exactamente a la mitad entre el cero y el uno.

Ubicar una fracción en la recta numérica puede ser muy útil para comprender su valor en relación a otros números y para comparar distintas fracciones entre sí. A través de esta representación gráfica, podemos visualizar de manera clara y precisa la posición de una fracción en el contexto de la línea numérica.

Cómo identificar si una fracción se encuentra al lado izquierdo o derecho de otra fracción en una recta numérica

Para ubicar una fracción en una recta numérica, es importante saber si se encuentra al lado izquierdo o derecho de otra fracción. Esto nos ayudará a tener una mejor comprensión visual de la relación de las fracciones entre sí.

Paso 1: Identifica los extremos de la recta numérica

Lo primero que debemos hacer es identificar los extremos de la recta numérica. En la mayoría de los casos, el extremo izquierdo de la recta corresponde al número cero (0), mientras que el extremo derecho será un número entero determinado. Por ejemplo, si estamos trabajando con una recta numérica que va del 0 al 10, entonces tendríamos como extremo derecho el número 10.

Paso 2: Caso fracción igual o denominadores iguales

Si las dos fracciones que queremos comparar tienen el mismo numerador y denominador, entonces podemos determinar cuál es mayor o menor fácilmente. Si el numerador es el mismo pero el denominador es diferente, entonces tenemos que observar cuál es la fracción más pequeña o más grande.


Ejemplo:
1/4 < 1/2


• Podemos observar que en este caso el numerador es igual para ambas fracciones, pero el denominador es diferente.
• La fracción 1/2 es mayor que 1/4 porque está dividida en menos partes, lo que significa que cada parte representa una cantidad mayor.

Paso 3: Numeradores iguales o denominadores diferentes

Si las fracciones que queremos comparar tienen el mismo denominador pero diferentes numeradores, entonces podemos ubicarlas en la recta numérica de la siguiente manera:


Ejemplo:
1/4 y 3/4


• El denominador es igual para ambas fracciones, lo cual facilita su ubicación en la recta numérica.
• Dividimos la recta numérica en el número de partes correspondientes al denominador (en este caso, en 4 partes iguales).
• Ubicamos el primer numerador, en este caso, 1, en la parte correspondiente a la fracción 1/4.
• A continuación, ubicamos el segundo numerador, en este caso, 3, en la parte correspondiente a la fracción 3/4.
• Podemos observar que la fracción 3/4 se encuentra al lado derecho de 1/4 en la recta numérica.

Paso 4: Numeradores y denominadores diferentes

Si tanto los numeradores como los denominadores son diferentes, debemos seguir los siguientes pasos:

1. Encuentra un denominador común para ambas fracciones.
2. Convierte ambas fracciones a fracciones equivalentes con el denominador común.
3. Compara las fracciones y ubícalas en la recta numérica siguiendo los pasos anteriores.

Recuerda practicar con diferentes ejemplos para familiarizarte con el proceso de ubicar fracciones en una recta numérica. Una vez que entiendas cómo hacerlo, podrás identificar rápidamente si una fracción se encuentra al lado izquierdo o derecho de otra fracción.

Existen técnicas o trucos para recordar cómo ubicar fracciones en una recta numérica

Ubicar una fracción en una recta numérica puede parecer complicado al principio, pero existen técnicas y trucos que te ayudarán a hacerlo de manera fácil y rápida. Si estás aprendiendo sobre fracciones o necesitas repasar este tema, ¡has llegado al lugar indicado!

La recta numérica es una herramienta visual que nos permite representar números en una línea recta, facilitando la comparación y ubicación de diferentes valores. Al colocar una fracción en una recta numérica, podemos visualizar su posición con respecto a otros números y tener una mejor comprensión de su magnitud.

Paso 1: Identificar el denominador de la fracción

El primer paso para ubicar una fracción en una recta numérica es identificar su denominador. El denominador nos indica en cuántas partes iguales se divide la unidad entera. Por ejemplo, si tenemos la fracción 3/4, el denominador es 4, lo que significa que la unidad entera se divide en cuatro partes iguales.

Paso 2: Dividir la recta numérica en partes iguales

Una vez que hemos identificado el denominador, debemos dividir la recta numérica en el mismo número de partes iguales. En el caso de la fracción 3/4, dividiremos la recta en cuatro partes iguales.


<ul>
<li>Divide la recta numérica en partes iguales.</li>
<li>Por ejemplo, si tienes la fracción 3/4, divídelo en cuatro partes iguales.</li>
</ul>


Paso 3: Colocar la fracción en su posición correcta

Una vez que hemos dividido la recta numérica en partes iguales, es hora de ubicar nuestra fracción en la recta. Para ello, contaremos cuántas partes iguales nos indica el numerador de la fracción y colocaremos un punto o una línea sobre esa ubicación.


<ol>
<li>Cuenta las partes iguales según el numerador.</li>
<li>En el caso de la fracción 3/4, contaríamos tres partes iguales desde el inicio.</li>
<li>Coloca un punto o una línea sobre esa ubicación.</li>
</ol>


Y ¡listo! Ahora puedes ubicar una fracción en una recta numérica utilizando estos sencillos pasos. Recuerda practicar con diferentes fracciones para familiarizarte cada vez más con este proceso.

Para ubicar una fracción en una recta numérica necesitas identificar su denominador, dividir la recta en partes iguales, contar según el numerador de la fracción y colocar un punto o una línea sobre esa ubicación. ¡No olvides practicar y sentirte seguro en este proceso!

Qué hacer si la fracción contiene números negativos en una recta numérica

Cuando trabajamos con fracciones en una recta numérica, es posible encontrarnos con situaciones en las cuales los números involucrados son negativos. En estos casos, el procedimiento para ubicar la fracción en la recta numérica sigue siendo el mismo, aunque debemos tener en cuenta algunas consideraciones adicionales.

Para comenzar, recordemos que en una recta numérica, los números positivos se encuentran a la derecha del cero, mientras que los números negativos se ubican a la izquierda. El cero actúa como punto de referencia para ubicar todas las fracciones y números en general.

Entonces, si tenemos una fracción negativa, por ejemplo -1/4, el primer paso consiste en identificar el cero en la recta numérica. A partir de ahí, trazamos una línea horizontal hacia la izquierda, considerando que cada unidad de distancia representa una fracción unitaria.

En el caso de la fracción -1/4, nos desplazamos una cuarta parte hacia la izquierda desde el cero. Es importante recordar que al igual que con las fracciones positivas, también podemos utilizar subdivisiones de la misma para ubicar más precisamente la posición en la recta numérica.

Ejemplo práctico

Supongamos que queremos ubicar la fracción -3/5 en una recta numérica. Comenzamos ubicando el cero como punto de referencia y trazamos una línea horizontal hacia la izquierda.

Luego, dividimos esta línea en cinco partes iguales, ya que estamos trabajando con una fracción 5 en el denominador. Para ello, podemos utilizar subdivisiones de la misma longitud. Cada una de estas subdivisiones representa una quinta parte.

A continuación, iniciamos desde el cero y nos desplazamos tres quintas partes hacia la izquierda. Así, hemos ubicado la fracción -3/5 en nuestra recta numérica.

Consideraciones adicionales

Es importante tener en cuenta que cuando trabajamos con fracciones negativas en una recta numérica, estamos ordenando los números de mayor a menor. De esta manera, las fracciones más grandes se ubicarán más cerca del origen (cero) mientras que las fracciones más pequeñas se encontrarán más alejadas de este punto de referencia.

Por otro lado, si estamos trabajando con combinaciones de números negativos y positivos en una recta numérica, debemos ordenar estos números teniendo en cuenta también el valor absoluto, ya que el mismo nos indica la distancia de cada número al origen, sin considerar su signo.

Ubicar fracciones negativas en una recta numérica requiere seguir el mismo procedimiento que para fracciones positivas, pero considerando que debemos desplazarnos hacia la izquierda y que estaremos ordenando los números de mayor a menor. Además, recordar utilizar divisiones o subdiviones para obtener una mayor precisión en la ubicación de la fracción.

¿Cuál es la importancia de ubicar correctamente las fracciones en una recta numérica?

Ubicar correctamente las fracciones en una recta numérica es de vital importancia para comprender y visualizar de manera fácil y rápida la relación y el orden que existe entre diferentes números racionales. Es una herramienta fundamental en el estudio de las matemáticas y nos permite representar gráficamente las fracciones, lo cual facilita su comparación y operaciones matemáticas.

Al ubicar una fracción en una recta numérica, estamos situándola en un punto específico entre dos números enteros. Esto nos ayuda a entender dónde se encuentra esa fracción en relación con otros valores y cómo se relaciona con ellos en términos de magnitud.

Una de las ventajas de utilizar la recta numérica para ubicar las fracciones es que nos permite visualizarlas de manera clara y concreta. Al representar una fracción en la recta numérica, podemos ver su posición relativa respecto a otros números y tener una mejor comprensión de su valor.

Pasos para ubicar una fracción en una recta numérica

A continuación, te presentamos los pasos que debes seguir para poder ubicar una fracción en una recta numérica:

1. Paso 1: Identificar los números enteros de referencia: Antes de comenzar a ubicar la fracción en la recta numérica, es importante identificar los números enteros de referencia que delimitarán el extremo izquierdo y derecho de la recta numérica. Estos números generalmente son aquellos entre los cuales se encuentra la fracción que vamos a ubicar.
2. Paso 2: Dividir la recta numérica en partes iguales: Una vez que hemos identificado los números enteros de referencia, debemos dividir la recta numérica en partes iguales. El número de divisiones dependerá de la precisión que queramos utilizar al ubicar la fracción.
3. Paso 3: Localizar el punto correspondiente a la fracción: En este paso, visualizaremos la fracción y determinaremos su ubicación exacta en la recta numérica. Para ello, evaluaremos a qué distancia se encuentra la fracción del número entero izquierdo de referencia, contando las unidades de medida correspondientes a las divisiones realizadas.

Una vez que hemos seguido estos pasos, habremos logrado ubicar correctamente la fracción en la recta numérica. Este método nos permite representar gráficamente una fracción y tener una mejor comprensión de su valor en relación con otros números racionales.

Cómo puedes practicar y mejorar tus habilidades para ubicar fracciones en una recta numérica

Ubicar una fracción en una recta numérica puede parecer un desafío, especialmente si no estás familiarizado con los conceptos básicos de fracciones y rectas numéricas. Sin embargo, con la práctica y algunos consejos útiles, podrás dominar esta habilidad de manera fácil y rápida.

1. Comprende qué es una fracción

Antes de poder ubicar una fracción en una recta numérica, es importante comprender qué es una fracción y cómo se representa. Una fracción se compone de dos partes: el numerador y el denominador. El numerador indica cuántas partes se toman de un todo, mientras que el denominador indica en cuántas partes se divide el todo.

Por ejemplo, en la fracción 2/5, el numerador es 2 y el denominador es 5. Esto significa que estamos tomando dos partes de un todo dividido en cinco partes iguales.

2. Identifica los números de la recta numérica

Antes de poder ubicar la fracción en la recta numérica, debes identificar los números que componen la recta. Imagina que estás trabajando con una recta numérica del 0 al 1. En este caso, tendrías que identificar los puntos correspondientes a 0, 1/4, 1/2 y 3/4, por ejemplo.

Puedes marcar estos puntos en la recta numérica utilizando el método que prefieras. Algunas personas prefieren dibujar una línea y marcar los puntos con puntos o cruces, mientras que otras prefieren utilizar una escala más precisa.

3. Divide la recta numérica en partes iguales

Una vez que hayas identificado los puntos de la recta numérica, el siguiente paso es dividir la recta en partes iguales según el denominador de la fracción. Por ejemplo, si estás trabajando con una fracción que tiene un denominador de 5, deberás dividir la recta numérica en cinco partes iguales.

Puedes hacer esto marcando puntos igualmente espaciados en la recta numérica o utilizando una herramienta como una regla o una escala. Asegúrate de que cada parte sea igual en longitud y esté claramente marcada.

4. Ubica el numerador en la parte adecuada de la recta numérica

Ahora que has dividido la recta numérica en partes iguales, es hora de ubicar el numerador en el punto correspondiente de la recta. Si tienes una fracción como 2/5, deberás ubicar el punto que representa el número 2 en la segunda parte de la recta.

Para hacer esto, puedes contar las partes desde el punto inicial en la recta hasta llegar al punto correspondiente a tu numerador. En este caso, contarías dos partes desde el punto inicial para ubicar el número 2.

5. Marca la fracción en la recta numérica

Una vez que hayas ubicado el numerador en la parte adecuada de la recta numérica, puedes marcar la fracción completa en la recta. Utiliza algún símbolo o una línea para representar la fracción en su ubicación correspondiente.

Por ejemplo, para la fracción 2/5, podrías dibujar una línea diagonal que vaya desde el punto inicial de la recta hasta el punto correspondiente al numerador. Esta línea representaría la fracción 2/5 ubicada en la recta numérica.

Ahora que sabes cómo ubicar una fracción en una recta numérica, puedes practicar con diferentes ejemplos y fracciones. Recuerda que la práctica constante te ayudará a mejorar tus habilidades y a sentirte más cómodo al trabajar con fracciones y rectas numéricas. ¡No tengas miedo de cometer errores y sigue practicando!

Dónde más se utilizan las rectas numéricas en matemáticas y otras áreas

Las rectas numéricas son una herramienta fundamental en matemáticas, pero su utilidad no se limita solo a esta área. También son utilizadas en otras disciplinas como física, estadística y economía.

En física, las rectas numéricas son utilizadas para representar magnitudes físicas como velocidad, aceleración o distancia. Al ubicar estas magnitudes en la recta numérica, es posible visualizar su comportamiento y realizar comparaciones más fácilmente.

En estadística, las rectas numéricas se utilizan para representar datos y observaciones de manera gráfica. Esto facilita la interpretación de los resultados y permite identificar patrones o tendencias en los datos.

En economía, las rectas numéricas también son útiles para representar variables económicas como precios, demanda o oferta. De esta manera, es posible analizar las interacciones entre estas variables y comprender mejor el funcionamiento del mercado.

Además de estas áreas específicas, las rectas numéricas también pueden ser utilizadas en situaciones cotidianas. Por ejemplo, al planificar un viaje, se puede utilizar una recta numérica para calcular la distancia recorrida en diferentes etapas o estimar el tiempo que tomará llegar a un destino.

Las rectas numéricas tienen aplicaciones en diversas disciplinas, desde matemáticas hasta física, estadística y economía. Su uso facilita la representación y análisis de datos, así como la comprensión de conceptos abstractos en diferentes contextos.

Para ubicar una fracción en una recta numérica, se divide el segmento entre los números enteros que se encuentran antes y después de la fracción en partes iguales.

Para encontrar el punto medio de una fracción en una recta numérica, se suma el numerador y el denominador de la fracción y se divide entre 2.

Si una fracción está más cerca del número entero en la recta numérica, su valor es mayor que 0; si está más cerca del cero, su valor es menor que 0.

Una fracción impropia se representa en una recta numérica colocando el número entero parte de la fracción en la posición correspondiente y luego dividir el segmento restante en partes iguales según el denominador de la fracción.

No, solo se pueden representar en la recta numérica aquellas fracciones con numerador y denominador enteros. Las fracciones decimales no se pueden representar de manera exacta en una recta numérica.